题目内容
已知数列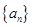 的通项公式为
的通项公式为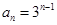 ,在等差数列数列
,在等差数列数列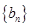 中,
中,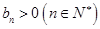 ,且
,且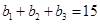 ,又
,又 、
、 、
、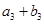 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前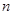 项和
项和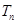 .
.
(1) ;(2)
;(2)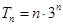 .
.
解析试题分析:(1)先由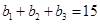 求出
求出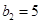 ,并根据数列
,并根据数列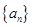 的通项公式求出前三项的值,并设数列
的通项公式求出前三项的值,并设数列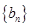 的公差为
的公差为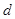 ,根据题中条件求出
,根据题中条件求出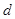 ,注意根据题中的条件对
,注意根据题中的条件对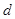 的值进行取舍,从而求出数列
的值进行取舍,从而求出数列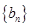 的通项公式,最终确定数列
的通项公式,最终确定数列 的通项公式;(2)在(1)的基础上,利用错位相减法求数列
的通项公式;(2)在(1)的基础上,利用错位相减法求数列 的前
的前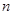 项和
项和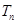 .
.
试题解析:(1)设等差数列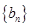 的公差为
的公差为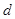 ,对任意
,对任意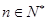 ,
,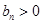 ,则
,则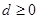 ,
,
由于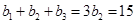 ,所以
,所以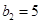 ,
, ,
,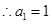 ,
,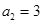 ,
,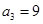 ,
,
因此 ,
, ,
,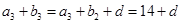 ,
,
由于 、
、 、
、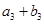 成等比数列,
成等比数列,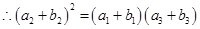 ,
,
即 ,整理得
,整理得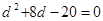 ,由于
,由于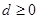 ,则
,则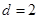 ,
,
而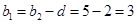 ,
, ,
,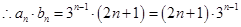 ;
;
(2)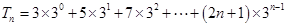 , ①
, ①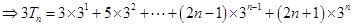 , ②
, ②
② ①得,
①得,

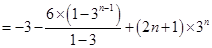
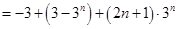
 ,
,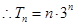 .
.
考点:1.利用基本量法求等差数列的通项;2.错位相减法求和

练习册系列答案
相关题目
 、
、 的每一项都是正数,
的每一项都是正数, ,
, ,且
,且 、
、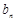 、
、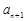 成等差数列,
成等差数列,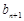 成等比数列,
成等比数列,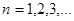 .
.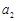 、
、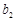 的值;
的值;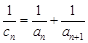 ,证明:对一切正整数
,证明:对一切正整数 ,有
,有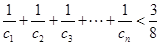 .
.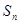 是各项均为非零实数的数列
是各项均为非零实数的数列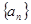 的前
的前 项和,给出如下两个命题上:
项和,给出如下两个命题上: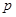 :
: :等式
:等式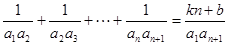 对任意
对任意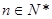 )恒成立,其中
)恒成立,其中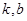 是常数。
是常数。 与
与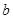 ,问
,问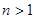 )和正数M,数列
)和正数M,数列 ,试求
,试求 中,公差
中,公差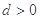 ,其前
,其前 项和为
项和为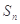 ,且满足:
,且满足: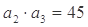 ,
, .
. ,
, ,求
,求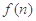 的最小值.
的最小值. 满足
满足 ,且对任意非负整数
,且对任意非负整数 均有:
均有: .
. ;
; 是等差数列,并求
是等差数列,并求 的通项;
的通项; ,求证:
,求证: .
.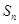 为数列
为数列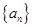 的前
的前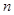 项和,且有
项和,且有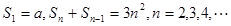
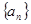 是单调递增数列,求
是单调递增数列,求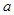 的取值范围.
的取值范围. 的前
的前 项和为
项和为 ,且
,且 ,数列
,数列 满足
满足 ,且点
,且点 在直线
在直线 上.
上. 的前
的前 .
.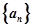 的前n项和为
的前n项和为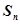 ,且
,且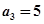 ,
,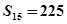 .
. 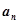 ;(2)设
;(2)设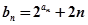 ,求数列
,求数列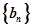 的前n项和
的前n项和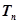 .
. 
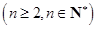 的两个数列
的两个数列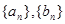 满足
满足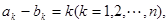 且集合
且集合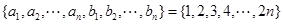 ,则称数列
,则称数列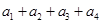 和
和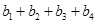 的值,并写出一对“
的值,并写出一对“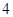 项
项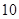 项相关数列”
项相关数列”