题目内容
函数f(x)=x3+ax2+bx+c,过曲线y=f(x)上的点P(1,f(1))的切线方程为y=3x+1;
(1)若y=f(x)在x=-2时有极值,求f(x)的表达式;
(2)在(1)的条件下,求y=f(x)在[-3,1]上的最大值;
(3)若函数y=f(x)在区间[-2,1]上单调递增,求b的取值范围。
(1)若y=f(x)在x=-2时有极值,求f(x)的表达式;
(2)在(1)的条件下,求y=f(x)在[-3,1]上的最大值;
(3)若函数y=f(x)在区间[-2,1]上单调递增,求b的取值范围。
解:(1)由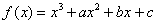 ,
,
求导数,得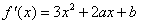 ,
,
过y=f(x)上点 P(1,f(1))的切线方程为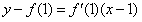 ,
,
即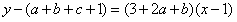 ,
,
而过y=f(x)上点P(1,f(1))的切线方程为y=3x+1,
故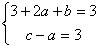 ,即
,即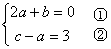 ,
,
∵y=f(x)在x=-2时有极值,
故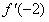 =0,∴-4a+b=-12, ③
=0,∴-4a+b=-12, ③
由①②③式,联立解得a=2,b=-4,c=5,
∴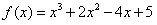 。
。
(2)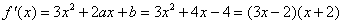 ,
,
见下表:

∴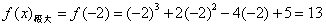 ,
,
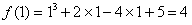 ,
,
∴f(x)在[-3,1]上最大值为13。
(3)y=f(x)在区间 [-2,1]上单调递增,
又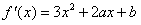 ,由(1)知2a+b=0,
,由(1)知2a+b=0,
∴ 依题意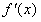 在[-2,1]上恒有
在[-2,1]上恒有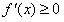 ,即
,即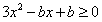 在[-2,1]上恒成立,
在[-2,1]上恒成立,
①当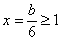 时,
时,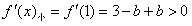 ,∴b≥6;
,∴b≥6;
②当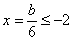 时,
时,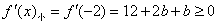 ,∴
,∴ ;
;
③当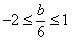 时,
时, ,∴0≤b≤6;
,∴0≤b≤6;
综合上述讨论可知,所求参数b取值范围是:b≥0。
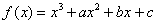 ,
,求导数,得
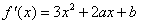 ,
,过y=f(x)上点 P(1,f(1))的切线方程为
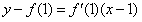 ,
,即
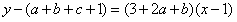 ,
,而过y=f(x)上点P(1,f(1))的切线方程为y=3x+1,
故
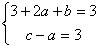 ,即
,即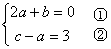 ,
,∵y=f(x)在x=-2时有极值,
故
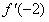 =0,∴-4a+b=-12, ③
=0,∴-4a+b=-12, ③ 由①②③式,联立解得a=2,b=-4,c=5,
∴
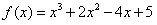 。
。(2)
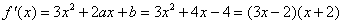 ,
,见下表:

∴
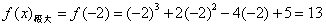 ,
,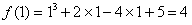 ,
,∴f(x)在[-3,1]上最大值为13。
(3)y=f(x)在区间 [-2,1]上单调递增,
又
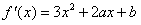 ,由(1)知2a+b=0,
,由(1)知2a+b=0,∴ 依题意
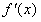 在[-2,1]上恒有
在[-2,1]上恒有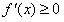 ,即
,即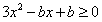 在[-2,1]上恒成立,
在[-2,1]上恒成立,①当
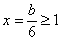 时,
时,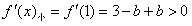 ,∴b≥6;
,∴b≥6;②当
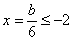 时,
时,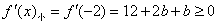 ,∴
,∴ ;
;③当
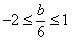 时,
时, ,∴0≤b≤6;
,∴0≤b≤6;综合上述讨论可知,所求参数b取值范围是:b≥0。

练习册系列答案
相关题目