Question

16．偶函数f（x）、奇函数g（x）的图象分别如图①、②所示，若方程：f（f（x））=0，f（g（x））=0，g（g（x））=2，g（f（x））=2的实数根的个数分别为a、b、c、d，则a+b+c+d=（　　）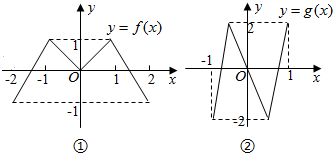

• A． 16
• B． 18
• C． 20
• D． 22

Answer 1

分析 结合函数图象把方程根的个数转化为函数图象的交点个数，可分别求得a，b，c，d进而可得答案．

解答 解：逐个考察下列方程
（1）f（f（x））=0，根的个数分析如下：
令f（x）=0解得x=0，-$\frac{3}{2}$，$\frac{3}{2}$（假设为$\frac{3}{2}$），再分别令f（x）=0，-$\frac{3}{2}$，$\frac{3}{2}$，
解的个数分别为，3，0，0，共3个，所以，a=3；
（2）f（g（x））=0，根的个数分析如下：
令f（x）=0解得x=0，-$\frac{3}{2}$，$\frac{3}{2}$，再分别令g（x）=0，-$\frac{3}{2}$，$\frac{3}{2}$，
解的个数分别为，3，3，3，共9个，所以，b=9；
（3）g（g（x））=2，根的个数分析如下：
令g（x）=2解得x=1，-$\frac{1}{2}$，（假设为-$\frac{1}{2}$），再分别令g（x）=1，-$\frac{1}{2}$，
解的个数分别为，3，3，共6个，所以，c=6；
（4）g（f（x））=2，根的个数分析如下：
令g（x）=2解得x=1，-$\frac{1}{2}$，再分别令f（x）=1，-$\frac{1}{2}$，
解的个数分别为，2，2，共4个，所以，d=4；
∴a+b+c+d=3+9+6+4=22，
故选：D．

点评 本题主要考查了函数的图象和性质，涉及函数的奇偶性、方程的根，以及数形结合的思想方法和推理能力与计算能力，属于难题．