题目内容

是否存在锐角α和β,使得下列两式①α+2β=,②tantanβ=2-同时成立?

解:假设存在符合题意的锐角α,β.

由①得+β=,

所以tan(+β)=.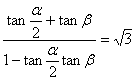

由②知tantanβ=2-,所以tan+tanβ=3-,

所以tan,tanβ是方程x2-(3-)x+2-=0的两个根,得x1=1,x2=2-.

因为0＜α＜,0＜＜,0＜tan＜1,

所以tan≠1,tan=2-,tanβ=1.

又因为0＜β＜,所以将β=代入①得α=.

所以存在锐角α=,β=,使①②同时成立.

练习册系列答案
相关题目
是否存在锐角α，β，使得下列两式：①α+2β=
2π
3
；②tan
α
2
?tanβ=2-
3
同时成立？若存在，求出α和β；若不存在，说明理由？
（1）是否存在锐角α与β，使得（1）α+2β=
2π
3
，（2）tan
α
2
•tanβ=2-
3
同时成立．
若存在，求出α和β的值；若不存在，说明理由．
（2）已知tanα，tanβ是方程x2-3x-3=0的两根，求sin2（α+β）-3sin（α+β）cos（α+β）-3cos2（α+β）的值．
是否存在锐角和,使得(1);(2)同时成立,若存在,求出、的值,若不存在,说明理由．
是否存在锐角α和β,使得(1)α+2β=,(2)tantanβ=2-同时成立?若存在,则求出α、β的值;若不存在,请说明理由.

是否存在锐角，使得（1）同时成立？若存在，求出和的值；若不存在，说明理由。

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网