题目内容
是否存在锐角α,β,使得下列两式:①α+2β=| 2π |
| 3 |
| α |
| 2 |
| 3 |
分析:由条件可得 tan
=1,tanβ=2-
,或tan
=2-
,tanβ=1,根据α,β为锐角,求出α,β 的值.
| α |
| 2 |
| 3 |
| α |
| 2 |
| 3 |
解答:解:由α+2β=
得:
+β=
,tan(
+β)=
=
.
将②式代入得:tan
+tanβ=3-
,与②式联立,解得:tan
=1,tanβ=2-
,
或tan
=2-
,tanβ=1.
当tan
=1时,因为0<
<
,这样的角α不存在,故只能是tan
=2-
,tanβ=1,
因为α,β均为锐角,所以α=
,β=
.
综上,存在锐角α=
,β=
,使得①,②同时成立.
| 2π |
| 3 |
| α |
| 2 |
| π |
| 3 |
| α |
| 2 |
tan
| ||
1-tan
|
| 3 |
将②式代入得:tan
| α |
| 2 |
| 3 |
| α |
| 2 |
| 3 |
或tan
| α |
| 2 |
| 3 |
当tan
| α |
| 2 |
| α |
| 2 |
| π |
| 4 |
| α |
| 2 |
| 3 |
因为α,β均为锐角,所以α=
| π |
| 6 |
| π |
| 4 |
综上,存在锐角α=
| π |
| 6 |
| π |
| 4 |
点评:本题考查两角和的正切公式,同角三角函数的基本关系,体现了分类讨论的数学思想,得到tan
=1,tanβ=2-
,或tan
=2-
,tanβ=1,是解题的关键.
| α |
| 2 |
| 3 |
| α |
| 2 |
| 3 |

练习册系列答案
相关题目
 ,使得(1)
,使得(1)
 同时成立?若存在,求出
同时成立?若存在,求出 和
和 的值;若不存在,说明理由。
的值;若不存在,说明理由。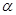 和
和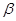 ,使得:
,使得: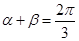 (2)
(2)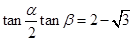 同时成立?
同时成立?