题目内容
(1)是否存在锐角α与β,使得(1)α+2β=| 2π |
| 3 |
| α |
| 2 |
| 3 |
若存在,求出α和β的值;若不存在,说明理由.
(2)已知tanα,tanβ是方程x2-3x-3=0的两根,求sin2(α+β)-3sin(α+β)cos(α+β)-3cos2(α+β)的值.
分析:(1)把条件1的等号两边都除以2得到
+β=
,两边取正切,利用两角和的正切函数公式及特殊角的三角函数值化简,并把①代入得到②,然后把①和②联立即可求出tan
和tanβ的值,利用特殊角的三角函数值求出角,根据α与β是锐角进行检验得到满足题意的α和β的值;
(2)因为tanα,tanβ是方程x2-3x-3=0的两根,所以根据根与系数的关系求出tanα+tanβ和tanαtanβ的值,然后利用两角和正切函数公式求出tan(α+β)的值,把所求的式子提取cos2(α+β)=
后得到关于tan(α+β)的关系式,把tan(α+β)的值代入即可求出值.
| α |
| 2 |
| π |
| 3 |
| α |
| 2 |
(2)因为tanα,tanβ是方程x2-3x-3=0的两根,所以根据根与系数的关系求出tanα+tanβ和tanαtanβ的值,然后利用两角和正切函数公式求出tan(α+β)的值,把所求的式子提取cos2(α+β)=
| 1 |
| 1+tan2(α+β) |
解答:解:(1)由α+2β=
得到
+β=
,所以tan(
+β)=
=tan
=
,
把tan
•tanβ=2-
①代入式子中得到:tan
+tanβ=3-
②,
把①②联立求得:tan
=1,tanβ=2-
或tan
=2-
,tanβ=1;
由题知锐角α,当tan
=1时,α=
矛盾,所以舍去;
当tanβ=1时,因为β为锐角,所以β=
,
根据α+2β=
得到α=
.
(2)因为tanα,tanβ是方程x2-3x-3=0的两根,根据根与系数的关系得到:tanα+tanβ=3,tanαtanβ=-3
则tan(α+β)=
=
,而原式=cos2(α+β)[tan2(α+β)-3tan(α+β)-3]
=
[tan2(α+β)-3tan(α+β)-3]=
[(
)2-3×
-3]=-3.
| 2π |
| 3 |
| α |
| 2 |
| π |
| 3 |
| α |
| 2 |
tan
| ||
1-tan
|
| π |
| 3 |
| 3 |
把tan
| α |
| 2 |
| 3 |
| α |
| 2 |
| 3 |
把①②联立求得:tan
| α |
| 2 |
| 3 |
| α |
| 2 |
| 3 |
由题知锐角α,当tan
| α |
| 2 |
| π |
| 2 |
当tanβ=1时,因为β为锐角,所以β=
| π |
| 4 |
根据α+2β=
| 2π |
| 3 |
| π |
| 6 |
(2)因为tanα,tanβ是方程x2-3x-3=0的两根,根据根与系数的关系得到:tanα+tanβ=3,tanαtanβ=-3
则tan(α+β)=
| tanα+tanβ |
| 1-tanαtanβ |
| 3 |
| 4 |
=
| 1 |
| 1+tan2(α+β) |
| 1 | ||
1+(
|
| 3 |
| 4 |
| 3 |
| 4 |
点评:考查学生灵活运用两角和与差的正切函数公式及同角三角函数间的基本关系化简求值,灵活运用韦达定理解决数学问题.是一道中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 ,使得(1)
,使得(1)
 同时成立?若存在,求出
同时成立?若存在,求出 和
和 的值;若不存在,说明理由。
的值;若不存在,说明理由。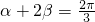 ,(2)
,(2)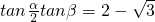 同时成立.
同时成立.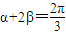 ,(2)
,(2)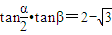 同时成立.
同时成立.