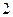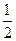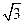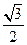题目内容
如图,在正方形ABCD中,E为AB中点,BF⊥CE于F,那么S△BFC:S正方形ABCD=( ).
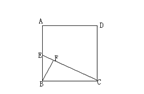
| A.1:3 | B.1:4 | C.1:5 | D.1:6 |

C.
分析:设正方形的边长为2a,利用勾股定理求出CE的长度,再根据相似三角形对应边成比例求出CF、BF的长度,然后求出△BFC的面积,最后求出与正方形面积的比值.
解:如图,设正方形的边长为2a,
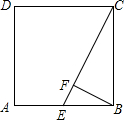
∵E是AB的中点,
BE=a,
CE=
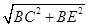 =
=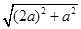 =
=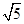 a,
a,∵BF⊥CE于F,
∴△BCE∽△FCB,
∴
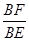 =
=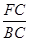 =
=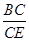 ,
,即
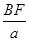 =
=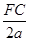 =
=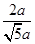 ,
,解得BF=
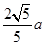 ,FC=
,FC=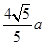 a,
a,所以S△BFC=
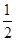 FC?BF=
FC?BF=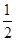 ×
×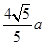 ×
×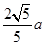 =
=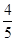 a2,
a2,S正方形ABCD=2a×2a=4a2,
∴S△BFC:S正方形ABCD=
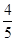 a2:4a2=1:5.
a2:4a2=1:5.故选B.

练习册系列答案
相关题目
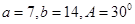 有两解
有两解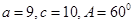 无解
无解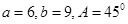 有两解
有两解 有一解
有一解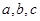 分别为三个内角A,B,C的对边,设向量
分别为三个内角A,B,C的对边,设向量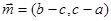 ,
,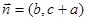 ,若
,若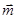 ⊥
⊥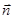 ,则角A的大小为
,则角A的大小为 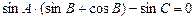 ,
,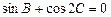 , 求:角A、B、C的大小。
, 求:角A、B、C的大小。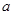 ,则DB=( )
,则DB=( )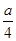
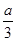
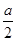
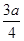
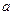 、
、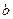 、
、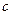 分别是
分别是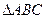 的三个内角
的三个内角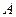 、
、
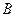 、
、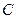 所对的边;(1) 若
所对的边;(1) 若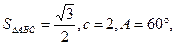 求
求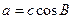 且
且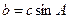 ,试判断
,试判断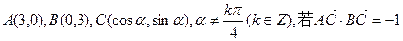
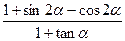 的值
的值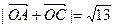 ,其中O是原点,且
,其中O是原点,且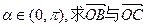 的夹角。
的夹角。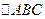 中,若
中,若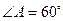 ,
,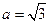 ,则
,则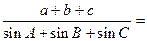 ( )
( )