题目内容
5.在平面直角坐标系中,若$\left\{\begin{array}{l}{x≤2}\\{x+y-2≥0}\\{x-y+2≥0}\end{array}\right.$,则$\sqrt{(x+1)^{2}+{y}^{2}}$的最小值是( )| A. | $\sqrt{5}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | 3 | D. | 5 |
分析 先画出满足条件的平面区域,根据$\sqrt{(x+1)^{2}+{y}^{2}}$的几何意义,从而求出其最小值.
解答 解:画出满足条件的平面区域,如图示: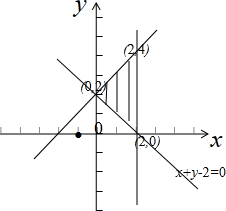 ,
,
显然,$\sqrt{(x+1)^{2}+{y}^{2}}$的最小值是(-1,0)到直线x+y-2=0的距离,
∴d=$\frac{|-1-2|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$,
故选:B.
点评 本题考察了简单的线性规划问题,考察数形结合思想,理解$\sqrt{(x+1)^{2}+{y}^{2}}$的几何意义是解答本题的关键,本题是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知集合M={1,2,3,4},N={2,4,5},则{x|x∈M∪N,x∉M∩N}=( )
| A. | {2,4,5} | B. | {1,3,5} | C. | {2,4} | D. | {1,2,3,4,5} |
20.已知函数f(x)=x3-mx,x∈R,若方程f(x)=2在x∈[-4,4]恰有3个不同的实数解,则实数m的取值范围是( )
| A. | $({-\frac{31}{2},3}]$ | B. | $({3,\frac{31}{2}}]$ | C. | $({-∞,-3})∪({\frac{31}{2},+∞})$ | D. | $({-∞,3})∪({\frac{31}{2},+∞})$ |
10.芜湖市区甲、乙、丙三所学校的高三文科学生共有800人,其中男、女生人数如下表:
从这三所学校的所有高三文科学生中随机抽取1人,抽到乙校高三文科女生的概率为0.2.
(Ⅰ)求表中x+z的值;
(Ⅱ)芜湖市五月份模考后,市教科所准备从这三所工作的所有高三文科学生中利用随机数表法抽取100人进行成绩统计分析,先将800人按001,002,…,800进行编号.如果从第8行第7列的数开始向右读,请你依次写出最先检测的3个人的编号;(下面摘取了随机数表中第7行至第9行)
8442 1753 3157 2455 0688 7704 7447 6721 7633 5026 8392
6301 5316 5916 9275 3816 5821 7071 7512 8673 5807 4439
1326 3321 1342 7864 1607 8252 0744 3815 0324 4299 7931
(Ⅲ)已知x≥145,z≥145,求丙校高三文科生中的男生比女生人数多的概率.
| 甲校 | 乙校 | 丙校 | |
| 男生 | 97 | 90 | x |
| 女生 | 153 | y | z |
(Ⅰ)求表中x+z的值;
(Ⅱ)芜湖市五月份模考后,市教科所准备从这三所工作的所有高三文科学生中利用随机数表法抽取100人进行成绩统计分析,先将800人按001,002,…,800进行编号.如果从第8行第7列的数开始向右读,请你依次写出最先检测的3个人的编号;(下面摘取了随机数表中第7行至第9行)
8442 1753 3157 2455 0688 7704 7447 6721 7633 5026 8392
6301 5316 5916 9275 3816 5821 7071 7512 8673 5807 4439
1326 3321 1342 7864 1607 8252 0744 3815 0324 4299 7931
(Ⅲ)已知x≥145,z≥145,求丙校高三文科生中的男生比女生人数多的概率.
17.已知M是抛物线C:y2=-4x上的一点,F为抛物线C的焦点,以MF为直径的圆与y轴相切于点(0,$\sqrt{3}$),则嗲M的横坐标为( )
| A. | -2 | B. | -3 | C. | -4 | D. | -2$\sqrt{3}$ |
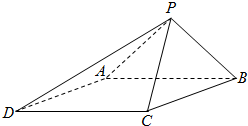 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.