题目内容
(本小题满分10分)选修41:几何证明选讲
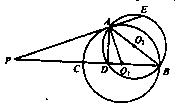
如图, 相交于A、B两点,AB是
相交于A、B两点,AB是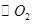 的直径,过A点作
的直径,过A点作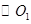 的切线交
的切线交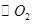 于点E,并与BO1的延长线交于点P,PB分别与
于点E,并与BO1的延长线交于点P,PB分别与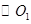 、
、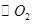 交于C,D两点.
交于C,D两点.
求证:(1)PA·PD=PE·PC;
(2)AD=AE
【答案】
见解析
【解析】(1)由切割线定理,易知 ,
, ,所以可得
,所以可得 .
.
(II) 连结 、
、 ,易证AC是圆O2的切线,再结合(1)的结论
,易证AC是圆O2的切线,再结合(1)的结论 ,可得
,可得 ,从而证明
,从而证明
 ,问题得证
,问题得证
(Ⅰ)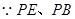 分别是⊙
分别是⊙ 的割线∴
的割线∴ 1 (2分)
1 (2分)
又 分别是⊙
分别是⊙ 的切线和割线∴
的切线和割线∴ 2 (4分)
2 (4分)
由1,2得 (5分)
(5分)
(Ⅱ)连结 、
、 ,
,

设 与
与 相交于点
相交于点
∵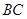 是⊙
是⊙ 的直径,∴
的直径,∴
∴ 是⊙
是⊙ 的切线.
(6分)
的切线.
(6分)
由(Ⅰ)知 ,∴
,∴ ∥
∥ ∴
∴ ⊥
⊥ ,
,  (8分)
(8分)
又∵ 是⊙
是⊙ 的切线,∴
的切线,∴ 
又 ,∴
,∴
∴ (10分)
(10分)

练习册系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,