题目内容
设函数
(1)求函数y=T(x2)和y=(T(x))2的解析式;
(2)是否存在实数a,使得T(x)+a2=T(x+a)恒成立,若存在,求出a的值,若不存在,请说明理由;
(3)定义Tn+1(x)=Tn(T(x)),且T1(x)=T(x),(n∈N*)
①当
 时,求y=T4(x)的解析式;
时,求y=T4(x)的解析式;已知下面正确的命题:当
 时(i∈N*,1≤i≤15),都有
时(i∈N*,1≤i≤15),都有 恒成立.
恒成立.②若方程T4(x)=kx恰有15个不同的实数根,确定k的取值;并求这15个不同的实数根的和.
【答案】分析:(1)先考虑讨论x2与 大小,然后把x2代入已知函数解析式中可求y=T(x2),对已知所给函数解析式直接进行平方可求y=(T(x))2的解析式;
大小,然后把x2代入已知函数解析式中可求y=T(x2),对已知所给函数解析式直接进行平方可求y=(T(x))2的解析式;
(2)分别求出T(x)+a2与T(x+a),代入使其对应项相等即可建立关于a的方程,可求
(3))①当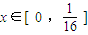 时,根据函数定义域的要求可知,
时,根据函数定义域的要求可知,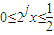 ,结合此规律寻求函数的递推规律可求故有
,结合此规律寻求函数的递推规律可求故有
②由①可知当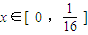 时,有T4(x)=16x,根据命题的结论可得,
时,有T4(x)=16x,根据命题的结论可得, ,代入可求,同理归纳可求
,代入可求,同理归纳可求
解答:解:(1)函数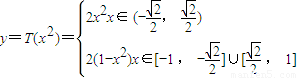
函数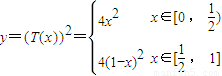 …4分
…4分
(2)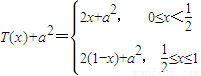 ,
,
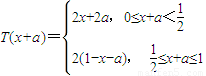 …6分
…6分
则当且仅当a2=2a且a2=-2a时,即a=0.
综上可知当a=0时,有T(x)+a2=T(x+a)=T(x)恒成立.…8分
(3)①当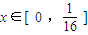 时,对于任意的正整数j∈N*,1≤j≤3,
时,对于任意的正整数j∈N*,1≤j≤3,
都有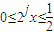 ,故有
,故有 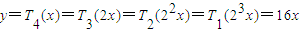 .…13分
.…13分
②由①可知当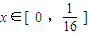 时,有T4(x)=16x,根据命题的结论可得,
时,有T4(x)=16x,根据命题的结论可得,
当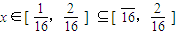 时,
时,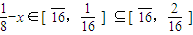 ,
,
故有 ,
,
因此同理归纳得到,当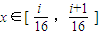 (i∈N,0≤i≤15)时,
(i∈N,0≤i≤15)时,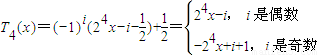 …15分
…15分
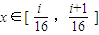 时,解方程T4(x)=kx得,
时,解方程T4(x)=kx得,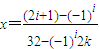
要使方程T4(x)=kx在x∈[0,1]上恰有15个不同的实数根,
则必须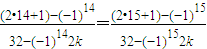 解得
解得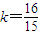
方程的根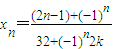 (n∈N*,1≤n≤15)…17分
(n∈N*,1≤n≤15)…17分
这15个不同的实数根的和为:S=x1+x2+…+x14+x15=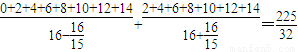 .…18分.
.…18分.
点评:本题以新定义为载体,主要考查了函数知识的综合应用,及逻辑推理、分析与运算的综合能力
 大小,然后把x2代入已知函数解析式中可求y=T(x2),对已知所给函数解析式直接进行平方可求y=(T(x))2的解析式;
大小,然后把x2代入已知函数解析式中可求y=T(x2),对已知所给函数解析式直接进行平方可求y=(T(x))2的解析式;(2)分别求出T(x)+a2与T(x+a),代入使其对应项相等即可建立关于a的方程,可求
(3))①当
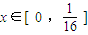 时,根据函数定义域的要求可知,
时,根据函数定义域的要求可知,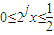 ,结合此规律寻求函数的递推规律可求故有
,结合此规律寻求函数的递推规律可求故有 ②由①可知当
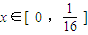 时,有T4(x)=16x,根据命题的结论可得,
时,有T4(x)=16x,根据命题的结论可得, ,代入可求,同理归纳可求
,代入可求,同理归纳可求解答:解:(1)函数
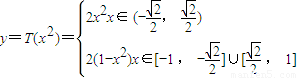
函数
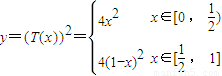 …4分
…4分(2)
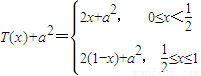 ,
,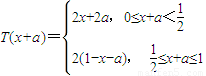 …6分
…6分则当且仅当a2=2a且a2=-2a时,即a=0.
综上可知当a=0时,有T(x)+a2=T(x+a)=T(x)恒成立.…8分
(3)①当
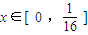 时,对于任意的正整数j∈N*,1≤j≤3,
时,对于任意的正整数j∈N*,1≤j≤3,都有
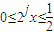 ,故有
,故有 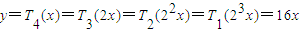 .…13分
.…13分②由①可知当
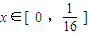 时,有T4(x)=16x,根据命题的结论可得,
时,有T4(x)=16x,根据命题的结论可得,当
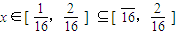 时,
时,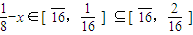 ,
,故有
 ,
,因此同理归纳得到,当
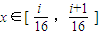 (i∈N,0≤i≤15)时,
(i∈N,0≤i≤15)时,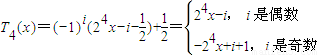 …15分
…15分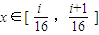 时,解方程T4(x)=kx得,
时,解方程T4(x)=kx得,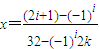
要使方程T4(x)=kx在x∈[0,1]上恰有15个不同的实数根,
则必须
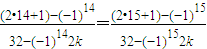 解得
解得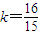
方程的根
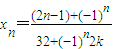 (n∈N*,1≤n≤15)…17分
(n∈N*,1≤n≤15)…17分这15个不同的实数根的和为:S=x1+x2+…+x14+x15=
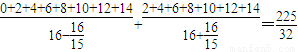 .…18分.
.…18分.点评:本题以新定义为载体,主要考查了函数知识的综合应用,及逻辑推理、分析与运算的综合能力

练习册系列答案
相关题目
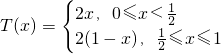
 x))和y=sin(
x))和y=sin( ]时,求y=Tn(x)的解析式;
]时,求y=Tn(x)的解析式;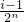 ,
,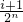 ](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(
](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(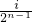 -x)恒成立.
-x)恒成立.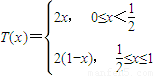
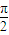 x))和y=sin(
x))和y=sin(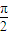 T(x))的解析式;
T(x))的解析式;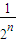 ]时,求y=Tn(x)的解析式;
]时,求y=Tn(x)的解析式;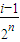 ,
,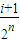 ](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(
](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(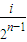 -x)恒成立.
-x)恒成立.