题目内容

抛物线y²=8x上一点P到焦点F的距离为6，在y轴上的射影为Q，O为原点，则四边形OFPQ的面积等于

A.
$数学公式$
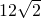
B.
$数学公式$
C.
20
D.
$数学公式$

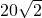
A
分析：先利用抛物线的定义，根据抛物线y²=8x上的点P到焦点F的距离为6，确定点P的横坐标，进而可得P的坐标，即可求得四边形OFPQ的面积．
解答：∵抛物线y²=8x上的点P（x，y）到焦点F的距离为6，
∴ $\text{[math]}$ +x=6，p=4，
∴x=4，
抛物线方程为y²=8x
∴x=4时，y=±4 $\text{[math]}$ ，
∴P的坐标为（4，±4 $\text{[math]}$ ）
∴四边形OFPQ是一个梯形，其面积为 $\text{[math]}$ （ $\text{[math]}$ +4）×4 $\text{[math]}$ =12 $\text{[math]}$ ，
故选A．
点评：本题考查抛物线的定义，考查四边形面积的计算，确定点P的位置是关键．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

抛物线y²=8x的焦点为F，A（4，-2）为一定点，在抛物线上找一点M，当|MA|+|MF|为最小时，则M点的坐标

，当||MA|-|MF||为最大时，则M点的坐标

已知双曲线

=1(a＞0，b＞0)的一条渐近线方程是y=

x，它的一个焦点在抛物线y²=8x的准线上，则双曲线的方程为（　　）

在下列四个命题中，
①如果一个命题的逆命题为真命题，那么它的否命题一定是真命题．
②方程

=1的图象表示双曲线的充要条件是k＜1或k＞2．
③过点M（2，4）作与抛物线y²=8x只有一个公共点的直线l有且只有一条．
④圆x²+y²=4上恰有三个点到直线4x-3y+5=0的距离为1．
正确的有

．（填序号）

（2012•丰台区一模）已知抛物线y²=8x上一点P到焦点的距离是6，则点P的坐标是

已知双曲线C：

=1(a＞0，b＞0)的左、右焦点分别是F₁、F₂，一条渐近线方程为y=x，抛物线y²=8x的焦点与双曲线C的右焦点重合，点P（

，y₀）在双曲线上．则