题目内容
△ABC中,下述表达式:(1)sin(A+B)+sinC;(2)cos(B+C)+cosA;(3)tan
tan
;(4)cos
sec
表示常数的是( )
| A+B |
| 2 |
| C |
| 2 |
| B+C |
| 2 |
| A |
| 2 |
分析:这类题适合用排除法.分析(1)不对后,即可排除A、B选项;又C、D两项都有(2),故(2)不用分析.
解答:解:∵(1)sin(A+B)+sinC=sin(π-C))+sinC=sinC+sinC=2sinC,不是常数.
∴排除答案A、B
∵(2)cos(B+C)+cosA=cos(π-A)+cosA=-cosA+cosA=0
∴(2)cos(B+C)+cosA是常数.
又∵(3)tan
tan
=tan(
-
)tan
=cot
tan
=1,
∴(3)tan
tan
是常数.
∵(4)cos
sec
=cos(
-
)sec
=
∴(4)cos
sec
不是常数
故答案选C
∴排除答案A、B
∵(2)cos(B+C)+cosA=cos(π-A)+cosA=-cosA+cosA=0
∴(2)cos(B+C)+cosA是常数.
又∵(3)tan
| A+B |
| 2 |
| C |
| 2 |
| π |
| 2 |
| C |
| 2 |
| C |
| 2 |
| C |
| 2 |
| C |
| 2 |
∴(3)tan
| A+B |
| 2 |
| C |
| 2 |
∵(4)cos
| B+C |
| 2 |
| A |
| 2 |
| π |
| 2 |
| A |
| 2 |
| A |
| 2 |
sin
| ||
cos
|
∴(4)cos
| B+C |
| 2 |
| A |
| 2 |
故答案选C
点评:本题主要考查诱导公式的运用.属基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
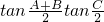 ;(4)
;(4)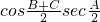 表示常数的是
表示常数的是