题目内容
给定区间D,对于函数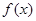 与
与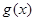 及任意
及任意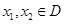 (其中
(其中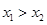 ),若不等式
),若不等式
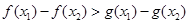 恒成立,则称函数
恒成立,则称函数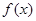 相对于函数
相对于函数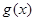 在区间D上是“渐先函数”.已知函数
在区间D上是“渐先函数”.已知函数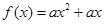 相对于函数
相对于函数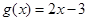 在区间[a,a+2]上是渐先函数,则实数
在区间[a,a+2]上是渐先函数,则实数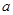 的取值范围是
.
的取值范围是
.
【答案】
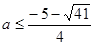 或
或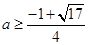
【解析】因为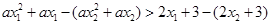 ,所以
,所以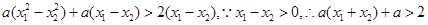 ,
,
所以当
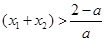 恒成立,因为
恒成立,因为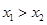 ,
,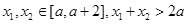 ,所以
,所以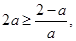 解得
解得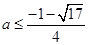 或
或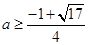 。即
。即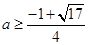 ;
;
当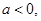
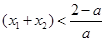 恒成立,因为
恒成立,因为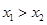 ,
,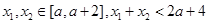 ,所以
,所以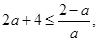 解得
解得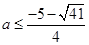 或
或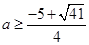 。即
。即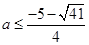 ;综上
;综上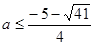 或
或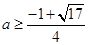 。
。

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
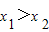 ),若不等式f(x1)-f(x2)>g(x1)-g(x2)恒成立,则称函数f(x)相对于函数g(x)在区间D上是“渐先函数”.已知函数f(x)=ax2+ax相对于函数g(x)=2x-3在区间[a,a+2]上是渐先函数,则实数a的取值范围是 .
),若不等式f(x1)-f(x2)>g(x1)-g(x2)恒成立,则称函数f(x)相对于函数g(x)在区间D上是“渐先函数”.已知函数f(x)=ax2+ax相对于函数g(x)=2x-3在区间[a,a+2]上是渐先函数,则实数a的取值范围是 .