题目内容
给定区间D,对于函数f(x)与g(x)及任意x1,x2∈D(其中x1>
),若不等式f(x1)-f(x2)>g(x1)-g(x2)恒成立,则称函数f(x)相对于函数g(x)在区间D上是“渐先函数”.已知函数f(x)=ax2+ax相对于函数g(x)=2x-3在区间[a,a+2]上是渐先函数,则实数a的取值范围是
| x | 2 |
a≤
或a≥
-5-
| ||
| 4 |
-1+
| ||
| 2 |
a≤
或a≥
.-5-
| ||
| 4 |
-1+
| ||
| 2 |
分析:法一:由题意可得,(ax12+ax1)-(ax22+ax2)>(2x1-3)-(2x2-3)在[a,a+2]上恒成立(a≠0),结合x1>x2,分类讨论a的正负,可得当a>0时,a(2a+1)<a(x1+x2+1)<a(2a+5),当a<0时,2a2+5a≥2,分别求解不等式即可求解
法二:由已知及导数的定义可知
>
在[a,a+2]上恒成立,即f‘(x)>g’(x),分别对已知函数求导,即可求解
法二:由已知及导数的定义可知
| f(x1)-f(x2) |
| x1-x2 |
| g(x1)-g(x2) |
| x1-x2 |
解答:解:法一:由题意可得,(ax12+ax1)-(ax22+ax2)>(2x1-3)-(2x2-3)在[a,a+2]上恒成立(a≠0)
整理可得,a(x1-x2)(x1+x2)+a(x1-x2)>2(x1-x2)
∵x1>x2
∴x1-x2>0
∴a(x1+x2+1)>2在[a,a+2]恒成立
∴2a<x1+x2<2(a+2)
当a>0时,a(2a+1)<a(x1+x2+1)<a(2a+5)
∴2a2+a≥2,解可得a≥
当a<0时,2a2+a>a(x1+x2+1)>2a2+5a
∴2a2+5a≥2
解可得,a≤
综上可得,a≤
或a≥
故答案为:a≤
或a≥
法二:由题意可得f(x1)-f(x2)>g(x1)-g(x2)在[a,a+2]上恒成立,且a≠0
∵x1>x2
∴
>
在[a,a+2]上恒成立
∴f‘(x)>g’(x)
∴2ax+a>2在[a,a+2]上恒成立
即a(2x+1)>2在[a,a+2]上恒成立
①当a>0时,可得2a2+a≥2,解可得a≥
当a<0时,2a2+5a≥2
解可得,a≤
综上可得,a≤
或a≥
故答案为:a≤
或a≥
整理可得,a(x1-x2)(x1+x2)+a(x1-x2)>2(x1-x2)
∵x1>x2
∴x1-x2>0
∴a(x1+x2+1)>2在[a,a+2]恒成立
∴2a<x1+x2<2(a+2)
当a>0时,a(2a+1)<a(x1+x2+1)<a(2a+5)
∴2a2+a≥2,解可得a≥
| ||
| 4 |
当a<0时,2a2+a>a(x1+x2+1)>2a2+5a
∴2a2+5a≥2
解可得,a≤
-5-
| ||
| 4 |
综上可得,a≤
-5-
| ||
| 4 |
| ||
| 4 |
故答案为:a≤
-5-
| ||
| 4 |
| ||
| 4 |
法二:由题意可得f(x1)-f(x2)>g(x1)-g(x2)在[a,a+2]上恒成立,且a≠0
∵x1>x2
∴
| f(x1)-f(x2) |
| x1-x2 |
| g(x1)-g(x2) |
| x1-x2 |
∴f‘(x)>g’(x)
∴2ax+a>2在[a,a+2]上恒成立
即a(2x+1)>2在[a,a+2]上恒成立
①当a>0时,可得2a2+a≥2,解可得a≥
| ||
| 4 |
当a<0时,2a2+5a≥2
解可得,a≤
-5-
| ||
| 4 |
综上可得,a≤
-5-
| ||
| 4 |
| ||
| 4 |
故答案为:a≤
-5-
| ||
| 4 |
| ||
| 4 |
点评:本题以新定义为载体,主要考查了函数的恒成立问题的求解,本题思路灵活,解法巧妙,注意体会掌握

练习册系列答案
相关题目
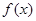 与
与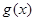 及任意
及任意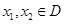 (其中
(其中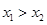 ),若不等式
),若不等式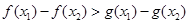 恒成立,则称函数
恒成立,则称函数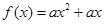 相对于函数
相对于函数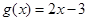 在区间[a,a+2]上是渐先函数,则实数
在区间[a,a+2]上是渐先函数,则实数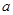 的取值范围是
.
的取值范围是
.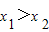 ),若不等式f(x1)-f(x2)>g(x1)-g(x2)恒成立,则称函数f(x)相对于函数g(x)在区间D上是“渐先函数”.已知函数f(x)=ax2+ax相对于函数g(x)=2x-3在区间[a,a+2]上是渐先函数,则实数a的取值范围是 .
),若不等式f(x1)-f(x2)>g(x1)-g(x2)恒成立,则称函数f(x)相对于函数g(x)在区间D上是“渐先函数”.已知函数f(x)=ax2+ax相对于函数g(x)=2x-3在区间[a,a+2]上是渐先函数,则实数a的取值范围是 .