题目内容
已知函数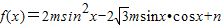 的定义域为
的定义域为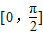 ,值域为[-5,4].试求函数g(x)=msinx+2ncosx(x∈R)的最小正周期和最值.
,值域为[-5,4].试求函数g(x)=msinx+2ncosx(x∈R)的最小正周期和最值.
【答案】分析:由辅助解公式,正弦型函数的性质,根据函数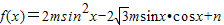 的定义域为
的定义域为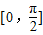 ,值域为[-5,4].我们易构造关于m,n的方程组,解方程组即可得到函数g(x)=msinx+2ncosx的解析式,进而得到函数g(x)=msinx+2ncosx(x∈R)的最小正周期和最值.
,值域为[-5,4].我们易构造关于m,n的方程组,解方程组即可得到函数g(x)=msinx+2ncosx的解析式,进而得到函数g(x)=msinx+2ncosx(x∈R)的最小正周期和最值.
解答:解: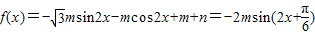 +m+n
+m+n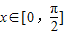
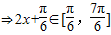
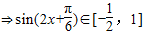
当m>0时,f(x)max=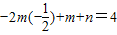 ,f(x)min=-m+n=-5
,f(x)min=-m+n=-5
解得m=3,n=-2,
从而,g(x)=3sinx-4cosx=5sin(x+φ)(x∈R),
T=2π,最大值为5,最小值为-5;
当m<0时,解得m=-3,n=1,
从而, ,T=2π,最大值为
,T=2π,最大值为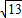 ,
,
最小值为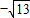 .
.
点评:本题考查三角函数的运算.考查的知识点有和差化积、周期与三角函数值域的求法、分类讨论的思想方法.近几年三角运算一直是考试所要求的基本题型之一,本题就是基于这一要求而制定的.
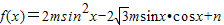 的定义域为
的定义域为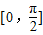 ,值域为[-5,4].我们易构造关于m,n的方程组,解方程组即可得到函数g(x)=msinx+2ncosx的解析式,进而得到函数g(x)=msinx+2ncosx(x∈R)的最小正周期和最值.
,值域为[-5,4].我们易构造关于m,n的方程组,解方程组即可得到函数g(x)=msinx+2ncosx的解析式,进而得到函数g(x)=msinx+2ncosx(x∈R)的最小正周期和最值.解答:解:
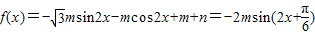 +m+n
+m+n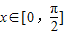
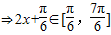
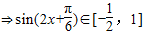
当m>0时,f(x)max=
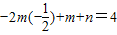 ,f(x)min=-m+n=-5
,f(x)min=-m+n=-5解得m=3,n=-2,
从而,g(x)=3sinx-4cosx=5sin(x+φ)(x∈R),
T=2π,最大值为5,最小值为-5;
当m<0时,解得m=-3,n=1,
从而,
 ,T=2π,最大值为
,T=2π,最大值为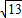 ,
,最小值为
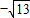 .
.点评:本题考查三角函数的运算.考查的知识点有和差化积、周期与三角函数值域的求法、分类讨论的思想方法.近几年三角运算一直是考试所要求的基本题型之一,本题就是基于这一要求而制定的.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数 的命题:
的命题:
①函数 在
在 上是减函数;②如果当
上是减函数;②如果当 时,
时, 最大值是
最大值是 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
 的定义域为
的定义域为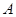 ,
,  ,且
,且 的真子集,求实数
的真子集,求实数 的取值范围.
的取值范围.




 的定义域为
的定义域为 ,且
,且 ,
, 为
为 ,
, 满足
满足 ,则
,则 的取值范围是
的取值范围是
 B.
B. C.
C. D.
D.