题目内容
已知函数的定义域为(0,+∞),且单调递增,满足f(4)=1,f(xy)=f(x)+f(y).
(Ⅰ)证明:f(1)=0;
(Ⅱ)若f(x)+f(x-3)≤1,求x的取值范围.
(Ⅰ)证明:f(1)=0;
(Ⅱ)若f(x)+f(x-3)≤1,求x的取值范围.
分析:(Ⅰ)令x=y=1即证f(1)=0;
(Ⅱ)依题意,可求f(x(x-3))<f(4),利用函数的定义域为(0,+∞),且单调递增,即可求得x的取值范围.
(Ⅱ)依题意,可求f(x(x-3))<f(4),利用函数的定义域为(0,+∞),且单调递增,即可求得x的取值范围.
解答:解:(Ⅰ)令x=y=1,则f(1×1)=f(1)+f(1),
∴f(1)=0;
(Ⅱ)∵f(4)=1,f(xy)=f(x)+f(y),
∴f(x)+f(x-3)≤1=f(4)?f(x(x-3))≤f(4),
∵函数的定义域为(0,+∞),且单调递增,
∴
,解得3<x≤4,
∴x的取值范围为(3,4].
∴f(1)=0;
(Ⅱ)∵f(4)=1,f(xy)=f(x)+f(y),
∴f(x)+f(x-3)≤1=f(4)?f(x(x-3))≤f(4),
∵函数的定义域为(0,+∞),且单调递增,
∴
|
∴x的取值范围为(3,4].
点评:本题考查抽象函数及其应用,着重考查赋值法即函数单调性的性质,考查解不等式组的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数 的命题:
的命题:
①函数 在
在 上是减函数;②如果当
上是减函数;②如果当 时,
时, 最大值是
最大值是 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
 的定义域为
的定义域为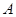 ,
,  ,且
,且 的真子集,求实数
的真子集,求实数 的取值范围.
的取值范围.




 的定义域为
的定义域为 ,且
,且 ,
, 为
为 ,
, 满足
满足 ,则
,则 的取值范围是
的取值范围是
 B.
B. C.
C. D.
D.