题目内容
13.设α,β为互不重合的平面,m,n是互不重合的直线,给出下列四个命题:①若n⊥β,m∥n,n?α,则m∥α;
②若m?α,n?α,m∥β,n∥β,则α∥β;
③若α∥β,m?α,n?β,则m∥n;
④若α⊥β,α∩β=m,n?α,n⊥m;
其中正确命题的序号为④.
分析 利用线面的关系,结合图形逐步判断:①中线面关系,由若n⊥β,m∥n,知m⊥β,则m∥α或m?α;
②面面平行的判定定理:一个平面内两条交线和另一平面平行,则这两平面平行;
③线线位置关系考查:相交,平行和异面,由题知不平行;
④线面垂直的判定定理.
解答 解:①若n⊥β,m∥n,n?α,则m∥α或m?α,故A错误;
②若m?α,n?α,m∥β,n∥β,且m,n相交,则α∥β,故B错误;
③若α∥β,m?α,n?β,则m,n没有交点,所以平行或异面,故C错误;
④若α⊥β,α∩β=m,n?α,n⊥m,则n⊥β,故D正确.
故答案为④.
点评 考查了线面,线线的位置关系,应紧扣定理,性质,不能随意猜测.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
4.已知角α终边上一点P的坐标是(2sin2,-2cos2),则sinα等于( )
| A. | sin2 | B. | -sin2 | C. | cos2 | D. | -cos2 |
1.函数f(x)是定义在R上偶函数,当x≥0时,f(x)单调递减.则下列各式成立的是( )
| A. | f(1)<f(-3) | B. | f(3)>f(2) | C. | f(-2)>f(3) | D. | f(2)>f(0) |
18.设集合A={a,b},则满足A∪B={a,b,c}的集合B的个数为( )
| A. | 8 | B. | 4 | C. | 3 | D. | 1 |
2.若f(x+y)=f(x)+f(y)+2xy(x,y∈R),f(1)=2,则f(-3)=( )
| A. | 2 | B. | 3 | C. | 6 | D. | 9 |
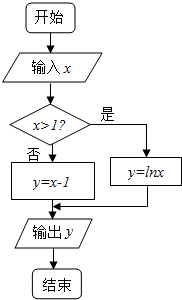 某算法的程序框图如图所示,则输出量y与输入量x满足的关系式是y=$\left\{\begin{array}{l}x-1,x≤1\\ lnx,x>1\end{array}\right.$.
某算法的程序框图如图所示,则输出量y与输入量x满足的关系式是y=$\left\{\begin{array}{l}x-1,x≤1\\ lnx,x>1\end{array}\right.$.