题目内容
已知函数f(x)=lg(ax2+2x+1),命题p:若f(x)的定义域为R,则0≤a≤1;命题q:若f(x)的值域为R,则0≤a≤1.那么
- A.p真q假
- B.p假q真
- C.“p或q”为假
- D.“p且q”为真
B
分析:在解答命题p时,由于函数f(x)的定义域是R,所以ax2+2x+1>0对一切x∈R成立.解此恒成立问题即可获得实数a的取值范围,再结合二次函数最值的知识易得函数f(x)的值域;对命题q由于函数f(x)的值域是R,所以u=ax2+2x+1的值域?(0,+∞).然后利用二次函数的图象与性质即可获得问题的解答.
解答:因为f(x)的定义域为R,所以ax2+2x+1>0对一切x∈R成立.
由此得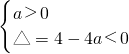
解得a>1.
又因为ax2+2x+1=a(x+ )2+1-
)2+1- >0,
>0,
所以f(x)=lg(ax2+2x+1)≥lg(1- ),
),
所以实数a的取值范围是(1,+∞),
故命题p是假命题.
(2)因为f(x)的值域是R,所以u=ax2+2x+1的值域?(0,+∞).
当a=0时,u=2x+1的值域为R?(0,+∞);
当a≠0时,u=ax2+2x+1的值域?(0,+∞)等价于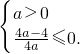
解之得0<a≤1
所以实数a的取值范围是[0.1].
故命题q是真命题.
故选B.
点评:本题考查对数函数的图象与性质问题.在解答的过程当中充分体现了恒成立的思想、问题转化的思想以及数形结合的思想.值得同学们体会和反思.
分析:在解答命题p时,由于函数f(x)的定义域是R,所以ax2+2x+1>0对一切x∈R成立.解此恒成立问题即可获得实数a的取值范围,再结合二次函数最值的知识易得函数f(x)的值域;对命题q由于函数f(x)的值域是R,所以u=ax2+2x+1的值域?(0,+∞).然后利用二次函数的图象与性质即可获得问题的解答.
解答:因为f(x)的定义域为R,所以ax2+2x+1>0对一切x∈R成立.
由此得
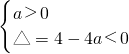
解得a>1.
又因为ax2+2x+1=a(x+
 )2+1-
)2+1- >0,
>0,所以f(x)=lg(ax2+2x+1)≥lg(1-
 ),
),所以实数a的取值范围是(1,+∞),
故命题p是假命题.
(2)因为f(x)的值域是R,所以u=ax2+2x+1的值域?(0,+∞).
当a=0时,u=2x+1的值域为R?(0,+∞);
当a≠0时,u=ax2+2x+1的值域?(0,+∞)等价于
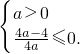
解之得0<a≤1
所以实数a的取值范围是[0.1].
故命题q是真命题.
故选B.
点评:本题考查对数函数的图象与性质问题.在解答的过程当中充分体现了恒成立的思想、问题转化的思想以及数形结合的思想.值得同学们体会和反思.

练习册系列答案
相关题目