题目内容
如果平面的一条斜线和它在这个平面上的射影的方向向量分别是
=（0，2，1），
=（
，
，
），那么这条斜线与平面的夹角是（ ）
| a |
| b |
| 2 |
| 5 |
| 5 |
| A、90° | B、60° |
| C、45° | D、30° |
分析：要求斜线与平面的夹角的大小，即分别求出斜线和它在这个平面上的射影的方向向量，然后利用向量的夹角公式即可求出向量的夹角，从而求出线面角的大小．
解答：解：∵斜线和它在这个平面上的射影的方向向量分别是
=（0，2，1），
=（
，
，
），
∴cosθ=
=
，→θ=30°．
因此
与
的夹角为30°．
故选D．
| a |
| b |
| 2 |
| 5 |
| 5 |
∴cosθ=
| ||||
|
|
| ||
| 2 |
因此
| a |
| b |
故选D．
点评：本小题要考查直线与平面所成的角、空间向量的夹角公式等基础知识，考查用空间向量解决立体几何问题的方法，考查空间想像能力．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
如果平面的一条斜线和它在这个平面上的射影的方向向量分别是
=（1，0，1），
=（0，1，1），那么这条斜线与平面所成的角是（ ）
| a |
| b |
| A、90° | B、60° |
| C、45° | D、30° |
那么这条斜线与平面所成的角是
____________ 
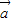=（1，0，1），
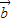=（0，1，1），那么这条斜线与平面所成的角是（ ）