题目内容
如果平面的一条斜线和它在这个平面上的射影的方向向量分别是
=(1,0,1),
=(0,1,1),那么这条斜线与平面所成的角是
| a |
| b |
60°
60°
.分析:这条斜线与平面所成的角就是两方向向量的夹角,故利用向量的夹角公式,即可求得结论.
解答:解:由题意,这条斜线与平面所成的角就是两方向向量的夹角.
∵
=(1,0,1),
=(0,1,1),
∴cos<
,
>=
=
=
∴<
,
>=60°
∴这条斜线与平面所成的角是60°
故答案为:60°
∵
| a |
| b |
∴cos<
| a |
| b |
| ||||
|
|
| 1 | ||||
|
| 1 |
| 2 |
∴<
| a |
| b |
∴这条斜线与平面所成的角是60°
故答案为:60°
点评:本题考查线面角,考查向量知识的运用,解题的关键是得到这条斜线与平面所成的角就是两方向向量的夹角.

练习册系列答案
相关题目
如果平面的一条斜线和它在这个平面上的射影的方向向量分别是
=(0,2,1),
=(
,
,
),那么这条斜线与平面的夹角是( )
| a |
| b |
| 2 |
| 5 |
| 5 |
| A、90° | B、60° |
| C、45° | D、30° |
如果平面的一条斜线和它在这个平面上的射影的方向向量分别是
=(1,0,1),
=(0,1,1),那么这条斜线与平面所成的角是( )
| a |
| b |
| A、90° | B、60° |
| C、45° | D、30° |
 那么这条斜线与平面所成的角是
____________
那么这条斜线与平面所成的角是
____________ 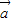 =(1,0,1),
=(1,0,1),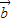 =(0,1,1),那么这条斜线与平面所成的角是( )
=(0,1,1),那么这条斜线与平面所成的角是( )