题目内容
【题目】某商场进行抽奖促销活动,抽奖箱中有大小完全相同的4个小球,分别标有“A”“B”“C”“D”.顾客从中任意取出1个球,记下上面的字后放回箱中,再从中任取1个球,重复以上操作,最多取4次,并规定若取出“D”字球,则停止取球.获奖规则如下:依次取到标有““A”“B”“C”“D”字的球为一等奖;不分顺序取到标有“A”“B”“C”“D”字的球,为二等奖;取到的4个球中有标有“A”“B”“C”三个字的球为三等奖.
(1)求分别获得一、二、三等奖的概率;
(2)设摸球次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() (2)见解析,
(2)见解析,![]()
【解析】
(1)设“摸到一等奖、二等奖、三等奖”分别为事件A,B,C,每次摸球相互独立,每个球被摸到的概率为![]() ,由事件的相互独立性性质求
,由事件的相互独立性性质求![]() ,先由排列方式计算事件B的基本事件个数,再由古典概型求概率方式求
,先由排列方式计算事件B的基本事件个数,再由古典概型求概率方式求![]() ,最后三等奖的情况有: “A,A,B,C”;“A,B,B,C”;“A,B,C,C”三种情况,由相互独立性求概率即可;
,最后三等奖的情况有: “A,A,B,C”;“A,B,B,C”;“A,B,C,C”三种情况,由相互独立性求概率即可;
(2)由相互独立性计算![]() 的取值为1、2、3、4时的概率,并列出对应的分布列,进而由均值计算公式求得均值.
的取值为1、2、3、4时的概率,并列出对应的分布列,进而由均值计算公式求得均值.
(1)设“摸到一等奖、二等奖、三等奖”分别为事件A,B,C,每次摸球相互独立,每个球被摸到的概率为![]() ,
,
则依次取到标有““A”“B”“C”“D”字的球的概率,![]() 不分顺序取到标有“A”“B”“C”“D”字的球时,前3次全排列“A”“B”“C”最后一次为“D”,再减去“一等奖”的1次,即基本事件有
不分顺序取到标有“A”“B”“C”“D”字的球时,前3次全排列“A”“B”“C”最后一次为“D”,再减去“一等奖”的1次,即基本事件有![]() 个,则概率
个,则概率![]()
三等奖的情况有: “A,A,B,C”;“A,B,B,C”;“A,B,C,C”三种情况.
则![]()
(2)设摸球的次数为![]() ,则
,则![]() 的可能取值为1、2、3、4.
的可能取值为1、2、3、4.
![]() ,
,![]() ,
,![]() ,
,![]()
故取球次数![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 |
|
|
|
|
|
所以数学期望为![]()

 习题精选系列答案
习题精选系列答案【题目】某生物研究所为研发一种新疫苗,在200只小白鼠身上进行科研对比实验,得到如下统计数据:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 30 |
|
|
注射疫苗 | 70 |
|
|
总计 | 100 | 100 | 200 |
现从未注射疫苗的小白鼠中任取1只,取到“感染病毒”的小白鼠的概率为![]() .
.
(Ⅰ)能否有![]() 的把握认为注射此种疫苗有效?
的把握认为注射此种疫苗有效?
(Ⅱ)在未注射疫苗且未感染病毒与注射疫苗且感染病毒的小白鼠中,分别抽取3只进行病例分析,然后从这6只小白鼠中随机抽取2只对注射疫苗情况进行核实,求抽到的2只均是注射疫苗且感染病毒的小白鼠的概率.
附: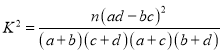 ,
,![]() ,
,
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |