题目内容
已知AB是异面直线a,b的公垂线段,AB=2,且a与b成30°角,在直线a上取AP=4,则点P到直线B的距离为( )A.2
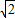
B.4
C.2
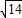
D.
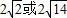
【答案】分析:过点B作直线BM∥a,过点P作MP⊥BM,过点M作MN⊥BN,连接PN,根据线面关系得到BN⊥平面PMN,即得到PN为点P到直线b的距离,再根据线段的长度关系利用解三角形的有关知识求出答案.
解答:解:过点B作直线BM∥a,过点P作MP⊥BM,过点M作MN⊥BN,连接PN,如图所示:
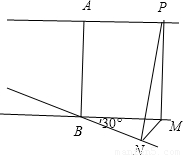
由以上可得:AB∥PM,AB=PM,所以AP=BM.
所以PM⊥平面BNM,
所以BN⊥MN,BN⊥PM,
所以BN⊥平面PMN,可得BN⊥PN,所以PN为点P到直线b的距离.
因为AP=4,所以BM=4.
因为∠MBN=30°,所以MN=2,
又因为PM=2,所以PN=2 .
.
故选A.
点评:本题主要考查异面直线上两点的距离问题,解决此类问题的关键是画出图象,再利用空间中的线面关系与解三角形的有关知识求解即可,此题属于中档题,对学生的空间想象能力要求较高.
解答:解:过点B作直线BM∥a,过点P作MP⊥BM,过点M作MN⊥BN,连接PN,如图所示:

由以上可得:AB∥PM,AB=PM,所以AP=BM.
所以PM⊥平面BNM,
所以BN⊥MN,BN⊥PM,
所以BN⊥平面PMN,可得BN⊥PN,所以PN为点P到直线b的距离.
因为AP=4,所以BM=4.
因为∠MBN=30°,所以MN=2,
又因为PM=2,所以PN=2
 .
.故选A.
点评:本题主要考查异面直线上两点的距离问题,解决此类问题的关键是画出图象,再利用空间中的线面关系与解三角形的有关知识求解即可,此题属于中档题,对学生的空间想象能力要求较高.

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
已知AB是异面直线a,b的公垂线段,AB=2,且a与b成30°角,在直线a上取AP=4,则点P到直线B的距离为( )
A、2
| ||||
| B、4 | ||||
C、2
| ||||
D、2
|