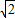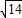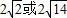题目内容
已知AB是异面直线a,b的公垂线段且A∈a,B∈b,AB=2,a与b成30°角,在a上取一点P,?¹AP=4,则P到b的距离等于( )
分析:作BC∥AP,PC⊥BC,PD⊥BD;在RT△CBD中求出CD;然后在RT△PCD中求出PD即可.
解答:解:
做BC∥AP,PC⊥BC,PD⊥BD,
∴PC=AB=2,AP=BC=4,
在RT△CBD中,BC=4,∠CDB=90°,∠CBD=30°.
∴CD=2,
在RT△PCD中,∠PCD=90°,
∴PD=
=2
.
故选:B.

做BC∥AP,PC⊥BC,PD⊥BD,
∴PC=AB=2,AP=BC=4,
在RT△CBD中,BC=4,∠CDB=90°,∠CBD=30°.
∴CD=2,
在RT△PCD中,∠PCD=90°,
∴PD=
| PC2+CD2 |
| 2 |
故选:B.
点评:本题主要考查异面直线及其所成的角的应用,考查计算能力和分析问题的能力.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
已知AB是异面直线a,b的公垂线段,AB=2,且a与b成30°角,在直线a上取AP=4,则点P到直线B的距离为( )
A、2
| ||||
| B、4 | ||||
C、2
| ||||
D、2
|