Question

使log₂（-x）＜x+1成立的x的取值范围是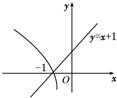

1. A.
   （-1，0）
2. B.
   [-1，0）
3. C.
   （-2，0）
4. D.
   [-2，0）

Answer 1

A
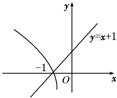
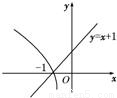
分析：根据负数没有对数得到-x大于0，求出x的范围，又根据y=log₂（-x），y=x+1的图象可知：对数函数值小于一次函数值，得到x大于-1，求出x范围的交集即为原不等式的解集．
解答：由对数函数y=log₂（-x），得到-x＞0，解得x＜0，
根据y=log₂（-x）和y=x+1的图象，且log₂（-x）＜x+1，得到x＞-1，
则满足条件的x∈（-1，0）．
故选A
点评：此题考查学生会利用函数图象的方法求其他不等式的解集，考查了数形结合的数学思想，是一道基础题．