题目内容
8．若f（x）=x2+2（a-1）x+2在区间（4，+∞）上是增函数，那么实数a的取值范围是（ ）| A． | a≥3 | B． | a≥-3 | C． | a≤-3 | D． | a≤5 |
分析 根据二次函数的单调性与开口方向和对称轴有关，先求出函数的对称轴，然后结合开口方向可知（4，+∞）是[1-a，+∞）的子集即可．
解答 解：二次函数f（x）=x2+2（a-1）x+2是开口向上的二次函数，
对称轴为x=1-a，
∴二次函数f（x）=x2+2（a-1）x+2在[1-a，+∞）上是增函数，
∵在区间（4，+∞）上是增函数，
∴1-a≤4，
解得：a≥-3．
故选B．
点评 本题主要考查了二次函数的单调性的运用，注意讨论对称轴和区间的关系，二次函数是高考中的热点问题，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
18．已知定义域为R的函数f（x）在区间（4，+∞）上为增函数，且函数y=f（x+4）为偶函数，则（ ）
| A． | f（3）＜f（6） | B． | f（3）＜f（5） | C． | f（2）＜f（3） | D． | f（2）＜f（5） |
13．已知集合A={x|log2x＜1}，B={y|y=2x，x∈A}，则A∩B=（ ）
| A． | （0，2） | B． | （1，2） | C． | [0，4） | D． | （1，4） |
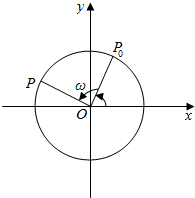将自行车支起来，使后轮能平稳地匀速运动，观察后轮气针的运动规律？若将后轮入如图所示的坐标系中，轮胎以角速度ωrad/s做圆周运动，P0是气针的初始位置，气针到原点O的距离为rcm，求气针P的纵坐标关于时间t的函数关系式，并求出P的运动周期，当φ=$\frac{π}{6}$，r=ω=1时，作出其函数的图象．