题目内容
 如图所示,在四面体P-ABC中,PA⊥BC,PB⊥AC,BC=2,PB=PC,P-BC-A是60°的二面角.
如图所示,在四面体P-ABC中,PA⊥BC,PB⊥AC,BC=2,PB=PC,P-BC-A是60°的二面角.(1)求证:PC⊥AB;
(2)求四面体P-ABC的体积.
分析:(1)作PO⊥面ABC于O,连接AO、BO.因为PA⊥BC,所以AO⊥BC,PB⊥AC,BO⊥AC,故O是△ABC的垂心.由此能够证明PC⊥AB.
(2)延长AO交BC于D,得AD⊥BC,故PD⊥BC,所以∠PDO是面PBC与面ABC所成角的平面角.因为PB=PC,所以D是BC的中点,故AB=AC.在Rt△PDO中,PO=ODtan60°=
OD.在Rt△ADC与Rt△CDO中,因为∠DAC=∠DCO,所以△ADC∽△CDO,由此能够求出P-ABC的体积.
(2)延长AO交BC于D,得AD⊥BC,故PD⊥BC,所以∠PDO是面PBC与面ABC所成角的平面角.因为PB=PC,所以D是BC的中点,故AB=AC.在Rt△PDO中,PO=ODtan60°=
| 2 |
解答: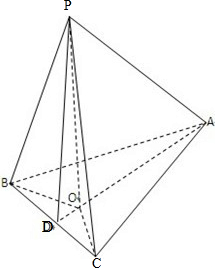 (1)证明:作PO⊥面ABC于O,连接AO、BO.
(1)证明:作PO⊥面ABC于O,连接AO、BO.
因为PA⊥BC,
所以AO⊥BC,PB⊥AC,BO⊥AC,
故O是△ABC的垂心.
连接CO,有CO⊥AB,
∵
,
∴AB⊥面POC,
∵PC?面POC,
所以PC⊥AB. (5分)
(2)解:延长AO交BC于D,
得AD⊥BC,
故PD⊥BC,
所以∠PDO是面PBC与面ABC所成角的平面角. (7分)
因为PB=PC,
所以D是BC的中点,
∵BC=2,
∴CD=1.
故AB=AC.
在Rt△PDO中,PO=ODtan60°=
OD. (9分)
在Rt△ADC与Rt△CDO中,
因为∠DAC=∠DCO,
所以△ADC∽△CDO,
故有
=
,
即AD•OD=CD2=(
)2=
•22═1 (11分)
∴P-ABC的体积:
V=
•PO•S△ABC
=
(
OD)•
•BC•AD
=
•
•2•(
OD)•AD
=
OD•AD
=
. (13分)
 (1)证明:作PO⊥面ABC于O,连接AO、BO.
(1)证明:作PO⊥面ABC于O,连接AO、BO.因为PA⊥BC,
所以AO⊥BC,PB⊥AC,BO⊥AC,
故O是△ABC的垂心.
连接CO,有CO⊥AB,
∵
|
∴AB⊥面POC,
∵PC?面POC,
所以PC⊥AB. (5分)
(2)解:延长AO交BC于D,
得AD⊥BC,
故PD⊥BC,
所以∠PDO是面PBC与面ABC所成角的平面角. (7分)
因为PB=PC,
所以D是BC的中点,
∵BC=2,
∴CD=1.
故AB=AC.
在Rt△PDO中,PO=ODtan60°=
| 3 |
在Rt△ADC与Rt△CDO中,
因为∠DAC=∠DCO,
所以△ADC∽△CDO,
故有
| AD |
| CD |
| CD |
| OD |
即AD•OD=CD2=(
| BC |
| 2 |
| 1 |
| 4 |
∴P-ABC的体积:
V=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
=
| ||
| 3 |
=
| ||
| 3 |
点评:本题考查直线与直线垂直的证明和体积的计算,解题时要认真审题,恰当地连接辅助线,注意合理地反立体几何问题转化为平面几何问题进行求解.易错点是空间思维能力有待于进一步加强.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
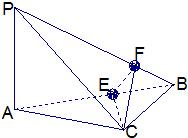 如图所示,在四面体P-ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=2
如图所示,在四面体P-ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=2
 ,PB=10,F是线段PB上一点,
,PB=10,F是线段PB上一点, ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.
 ,F是线段PB上一点,CF=
,F是线段PB上一点,CF=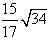 ,点E在线段AB上,且EF⊥PB,
,点E在线段AB上,且EF⊥PB, 