题目内容
已知直线l:x-y-1=0和圆C: (θ为参数,θ∈R),则直线l与圆C的位置关系为( )
(θ为参数,θ∈R),则直线l与圆C的位置关系为( )A.直线与圆相交
B.直线与圆相切
C.直线与圆相离
D.直线与圆相交但不过圆心
【答案】分析:化圆的参数方程为普通方程,求出圆的圆心坐标和半径,然后由点到直线的距离公式求出圆心到直线的距离,和半径比较后即可得到结论.
解答:解:由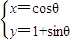 (θ为参数,θ∈R),得x2+(y-1)2=1.
(θ为参数,θ∈R),得x2+(y-1)2=1.
所以给出的圆C的圆心是(0,1),半径为1.
又直线l:x-y-1=0,由点到直线的距离公式得到圆心到直线的距离d=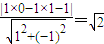 >1.
>1.
所以直线l与圆C的位置关系为相离.
故选C.
点评:本题考查了圆的参数方程,考查了直线和圆的位置关系,考查了点到直线的距离公式,是基础的计算题.
解答:解:由
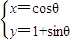 (θ为参数,θ∈R),得x2+(y-1)2=1.
(θ为参数,θ∈R),得x2+(y-1)2=1.所以给出的圆C的圆心是(0,1),半径为1.
又直线l:x-y-1=0,由点到直线的距离公式得到圆心到直线的距离d=
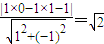 >1.
>1.所以直线l与圆C的位置关系为相离.
故选C.
点评:本题考查了圆的参数方程,考查了直线和圆的位置关系,考查了点到直线的距离公式,是基础的计算题.

练习册系列答案
相关题目