题目内容
偶函数 满足
满足 ,且在
,且在 时,
时, ,若直线
,若直线
 与函数
与函数 的图像有且仅有三个交点,则
的图像有且仅有三个交点,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
B
解析试题分析:因为 ,所以函数
,所以函数 的图像关于直线
的图像关于直线 对称,又
对称,又 是偶函数,所以
是偶函数,所以 ,即有
,即有 ,所以
,所以 是周期为2的函数,由
是周期为2的函数,由 ,得
,得 ,即
,即 ,画出函数
,画出函数 和直线
和直线 的示意图
的示意图
因为直线 与函数
与函数 的图像有且仅有三个交点,所以根据示意图易知:由直线
的图像有且仅有三个交点,所以根据示意图易知:由直线 与半圆
与半圆 相切,可计算得到
相切,可计算得到 ,由直线
,由直线 与半圆
与半圆 相切可计算得到
相切可计算得到 ,所以
,所以 ,选B.
,选B.
考点:1.函数的对称性、奇偶性、周期性;2.函数图像;3.直线与圆的位置关系;4.点到直线的距离公式.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
| A.a2-2a-16 |
| B.a2+2a-16 |
| C.-16 |
| D.16 |
函数 的递增区间是( )
的递增区间是( )
A.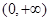 | B. | C. | D. |
若函数 的定义域是[0,4],则函数
的定义域是[0,4],则函数 的定义域是( )
的定义域是( )
| A.[ 0,2] | B.(0,2) | C.[0,2) | D.(0,2] |
 是定义在
是定义在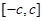 上的奇函数,其图象如图所示,令
上的奇函数,其图象如图所示,令 ,则下列关于函数
,则下列关于函数 的叙述正确的是()
的叙述正确的是()
A.若 ,则函数 ,则函数 的图象关于原点对称 的图象关于原点对称 |
B.若 ,则方程 ,则方程 有大于2的实根 有大于2的实根 |
C.若 ,则方程 ,则方程 有两个实根 有两个实根 |
D.若 ,则方程 ,则方程 有两个实根 有两个实根 |
已知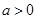 且
且 ,函数
,函数 满足对任意实数
满足对任意实数 ,都有
,都有 成立,则
成立,则 的取值范围是 ( )
的取值范围是 ( )
A. | B. ( ( | C. ( ( | D. |
函数 的零点是( )
的零点是( )
A. | B. | C. | D. |
 是定义在
是定义在 上的偶函数,且对任意
上的偶函数,且对任意 ,都有
,都有 ,当
,当 时,
时, ,设函数
,设函数 上的反函数为
上的反函数为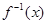 ,则
,则 的值为( )
的值为( ) 


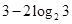
 ,则直线l的方程为( )
,则直线l的方程为( ) x+1
x+1