题目内容
两圆相交于点A(1,3)、B(m,-1),两圆的圆心均在直线x-y+c=0上,则m+c的值为( )
A.-1 B.3 C.2 D 0
C
解析考点:圆与圆的位置关系及其判定.
专题:综合题.
分析:根据题意可知,x-y+c=0是线段AB的垂直平分线,由垂直得到斜率乘积为-1,而直线x-y+c=0的斜率为1,所以得到过A和B的直线斜率为1,利用A和B的坐标表示出直线AB的斜率等于1,列出关于m的方程,求出方程的解即可得到m的值,然后利用中点公式和m的值求出线段AB的中点坐标,把中点坐标代入x-y+c=0中即可求出c的值,利用m和c的值求出m+c的值即可.
解答:解:由题意可知:直线x-y+c=0是线段AB的垂直平分线,又直线x-y+c="0" 的斜率为1,
则 =-1①,且
=-1①,且 -
-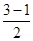 +c=0②,
+c=0②,
由①解得m=5,把m=5代入②解得c=-2,则m+c=5-2=3.
故选C
点评:此题考查学生掌握两圆相交时两圆心所在的直线是公共弦的垂直平分线,掌握两直线垂直时斜率所满足的关系,灵活运用中点坐标公式化简求值,是一道综合题

练习册系列答案
相关题目
两圆相交于点A(1,3)、B(m,-1),两圆的圆心均在直线x-y+c=0上,则m+c的值为( )
| A、-1 | B、2 | C、3 | D、0 |