题目内容
一直角梯形ABCD,AD是垂直于上、下底的腰,AB=2,CD=1,BC=| 3 |
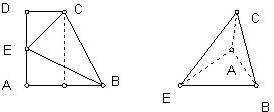
分析:由梯形ABCD为直角梯形,结合折叠后A与D重合,则所得三棱锥可以看成平面ABC为底面,以EA高,根据AB=2,CD=1,BC=
,E为AD的中点,我们利用海伦公式计算出三角形ABC的面积,及EA(高)的大小,代入三棱锥体积公式,即可得到答案.
| 3 |
解答:解:∵梯形ABCD为直角梯形
∴EA⊥AB,ED⊥CD
又∵折叠后A与D重合
故EA⊥AB,EA⊥CA
又∵AB∩CA=A
故EA⊥平面ABC
故所得三棱锥V=
•SABC•EA
又由AB=2,CD=1,BC=
,E为AD的中点,
我们易得:AD=
,即EA=
SABC=
=
∴V=
故答案:
.
∴EA⊥AB,ED⊥CD
又∵折叠后A与D重合
故EA⊥AB,EA⊥CA
又∵AB∩CA=A
故EA⊥平面ABC
故所得三棱锥V=
| 1 |
| 3 |
又由AB=2,CD=1,BC=
| 3 |
我们易得:AD=
| 2 |
| ||
| 2 |
SABC=
|
| ||
| 2 |
∴V=
| ||
| 12 |
故答案:
| ||
| 12 |
点评:本题考查的知识点是棱锥的体积与表面积计算,及棱锥的几何特征,根据已知确定三棱锥的底面和高是解答本题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
 已知四个面都是直角三角形的三棱锥,其中三个面展开后构成一直角梯形ABCD,如图AD⊥AB,AD⊥DC,AB=2,BC=
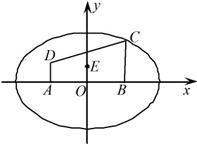
已知四个面都是直角三角形的三棱锥,其中三个面展开后构成一直角梯形ABCD,如图AD⊥AB,AD⊥DC,AB=2,BC=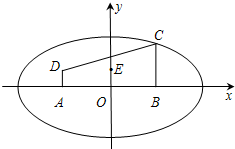 如图,在直角坐标系xOy中有一直角梯形ABCD,AB的中点为O,AD⊥AB,AD∥BC,AB=4,BC=3,AD=1,以A,B为焦点的椭圆经过点C.
如图,在直角坐标系xOy中有一直角梯形ABCD,AB的中点为O,AD⊥AB,AD∥BC,AB=4,BC=3,AD=1,以A,B为焦点的椭圆经过点C. 如图,一直角梯形ABCD,AB⊥AD,AD⊥DC,AB=2,
如图,一直角梯形ABCD,AB⊥AD,AD⊥DC,AB=2,