题目内容
定义a*b=
-ka-2,则方程x*x=0有唯一解时,实数k的取值范围是( )
| ab-1 |
分析:根据新定义,将方程x*x=0转化为无理方程
-kx-2=0有唯一解,分离成
=kx+2,利用方程两边的函数图象有唯一公共点,可以解出k的取值范围.
| x 2-1 |
| x 2-1 |
解答:解:由题中给出的定义,得方程x*x=0即
-kx-2=0,
移项得
=kx+2
作出函数y=
和y=kx+2的图象如下:
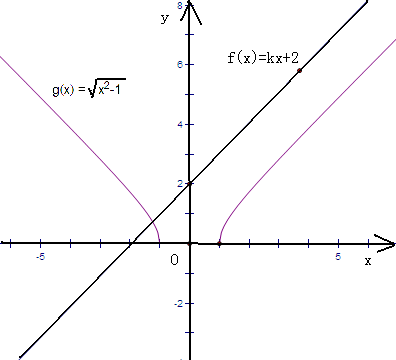
直线恒过点(0,2),当直线的斜率为±1时,直线与双曲线的渐近线平行,两个图象有唯一公共点,
当直线的斜率为±2时,直线过双曲线的顶点,刚好也是一个公共点,符合题意,
观察图象的变化,得直线的斜率的范围是k∈[-2,-1]∪[1,2]
故选B
| x 2-1 |
移项得
| x 2-1 |
作出函数y=
| x 2-1 |

直线恒过点(0,2),当直线的斜率为±1时,直线与双曲线的渐近线平行,两个图象有唯一公共点,
当直线的斜率为±2时,直线过双曲线的顶点,刚好也是一个公共点,符合题意,
观察图象的变化,得直线的斜率的范围是k∈[-2,-1]∪[1,2]
故选B
点评:本题着重考查了零点存在性以及函数与方程的知识点,属于基础题.读懂新定义,将方程转化为无理方程再用数形结合的方法,结合函数的图象解决是本题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目