题目内容
设双曲线![]() -
-![]() =1(a>0,b>0)的一条准线与两渐近线交于A,B两点,相应的焦点为F,若AF⊥BF,则双曲线的离心率为
=1(a>0,b>0)的一条准线与两渐近线交于A,B两点,相应的焦点为F,若AF⊥BF,则双曲线的离心率为
[ ]
A.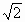
B.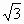
C.2
D.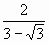
答案:A
解析:
解析:
|
|

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
题目内容
设双曲线![]() -
-![]() =1(a>0,b>0)的一条准线与两渐近线交于A,B两点,相应的焦点为F,若AF⊥BF,则双曲线的离心率为
=1(a>0,b>0)的一条准线与两渐近线交于A,B两点,相应的焦点为F,若AF⊥BF,则双曲线的离心率为
[ ]
|
|

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案