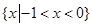题目内容
关于实数x的不等式|x- (a+1)2|≤
(a+1)2|≤ (a-1)2与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别为A,B.求使A⊆B成立的a的取值范围.
(a-1)2与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别为A,B.求使A⊆B成立的a的取值范围.
 (a+1)2|≤
(a+1)2|≤ (a-1)2与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别为A,B.求使A⊆B成立的a的取值范围.
(a-1)2与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别为A,B.求使A⊆B成立的a的取值范围.a=-1或1≤a≤3
由不等式|x- (a+1)2|≤
(a+1)2|≤ (a-1)2⇒
(a-1)2⇒
- (a-1)2≤x-
(a-1)2≤x- (a+1)2≤
(a+1)2≤ (a-1)2,
(a-1)2,
解得2a≤x≤a2+1,
于是A={x|2a≤x≤a2+1}.
由不等式x2-3(a+1)x+2(3a+1)≤0⇒(x-2)[x-(3a+1)]≤0,
①当3a+1≥2,即a≥ 时,B={x|2≤x≤3a+1},
时,B={x|2≤x≤3a+1},
因为A⊆B,所以必有
解得1≤a≤3;
②当3a+1<2,即a< 时,B={x|3a+1≤x≤2},
时,B={x|3a+1≤x≤2},
因为A⊆B,所以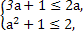
解得a=-1.
综上,使A⊆B的a的取值范围是a=-1或1≤a≤3.
 (a+1)2|≤
(a+1)2|≤ (a-1)2⇒
(a-1)2⇒-
 (a-1)2≤x-
(a-1)2≤x- (a+1)2≤
(a+1)2≤ (a-1)2,
(a-1)2,解得2a≤x≤a2+1,
于是A={x|2a≤x≤a2+1}.
由不等式x2-3(a+1)x+2(3a+1)≤0⇒(x-2)[x-(3a+1)]≤0,
①当3a+1≥2,即a≥
 时,B={x|2≤x≤3a+1},
时,B={x|2≤x≤3a+1},因为A⊆B,所以必有

解得1≤a≤3;
②当3a+1<2,即a<
 时,B={x|3a+1≤x≤2},
时,B={x|3a+1≤x≤2},因为A⊆B,所以
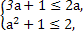
解得a=-1.
综上,使A⊆B的a的取值范围是a=-1或1≤a≤3.

练习册系列答案
相关题目
 ,则a-b=________.
,则a-b=________.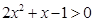 的解集为
的解集为 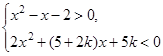 的解集中所含整数解只有-2,求
的解集中所含整数解只有-2,求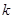 的取值范围 .
的取值范围 .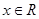 ,使
,使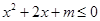 ”是假命题,求得
”是假命题,求得 的取值范围是
的取值范围是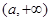 ,则实数
,则实数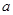 的值是__________.
的值是__________. 的解集为( )
的解集为( )