题目内容
若F1、F2分别为双曲线 -=1下、上焦点,O为坐标原点,P在双曲线的下支上,点M在上准线上,且满足: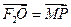 ,
,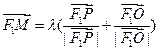
(1)求此双曲线的离心率;
(2)若此双曲线过N(,2),求此双曲线的方程
(3)若过N(,2)的双曲线的虚轴端点分别B1,B2(B2在x轴正半轴上),点A、B在双曲线上,且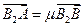 ,求
,求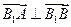 时,直线AB的方程.
时,直线AB的方程.
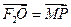 ,
,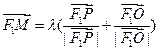
(1)求此双曲线的离心率;
(2)若此双曲线过N(,2),求此双曲线的方程
(3)若过N(,2)的双曲线的虚轴端点分别B1,B2(B2在x轴正半轴上),点A、B在双曲线上,且
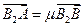 ,求
,求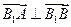 时,直线AB的方程.
时,直线AB的方程.(1) e="2;(2)" 双曲线的方程为-=1;(3) AB的方程为y=±(x-3) .
(1) 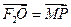
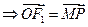 ,∴PF1OM为平行四边形,
,∴PF1OM为平行四边形,
又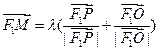 知M在∠PF1O的角平分线上,
知M在∠PF1O的角平分线上,
∴四边形PF1OM为菱形,且边长为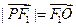 =c
=c
∴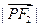 =2a+
=2a+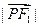 =2a+c,由第二定义=e即=e,∴+1=e且e>1
=2a+c,由第二定义=e即=e,∴+1=e且e>1
∴e="2"
(2)由e=2,∴c=2a即b2=3a2,双曲线方程为 -=1
又N(,2)在双曲线上,∴-=1,∴a2=3∴双曲线的方程为-=1;
(3)由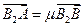 知AB过点B2,若AB⊥x轴,即AB的方程为x=3,此时AB1与BB1不垂直;设AB的方程为y=k(x-3)代入-=1得
知AB过点B2,若AB⊥x轴,即AB的方程为x=3,此时AB1与BB1不垂直;设AB的方程为y=k(x-3)代入-=1得
(3k2-1)x2-18k2x+27k2-9="0"
由题知3k2-1≠0且△>0即k2> 且k2≠,
设交点A(x1,y1),B(x2,y2),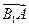 =(x1+3,y1),
=(x1+3,y1),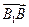 =(x2+3,y2),
=(x2+3,y2),
∵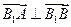 ,∴
,∴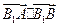 =0即x1x2+3(x1+x2)+9+y1y2=0
=0即x1x2+3(x1+x2)+9+y1y2=0
此时x1+x2=,x1·x2=9,
y1y2=k2(x1-3) (x2-3)=k2[x1x2-3(x1+x2)+9]= k2[18-]=-
∴9+3+9-=0,∴5 k2=1,∴k=±
∴AB的方程为y=±(x-3) .
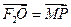
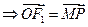 ,∴PF1OM为平行四边形,
,∴PF1OM为平行四边形,又
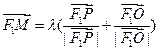 知M在∠PF1O的角平分线上,
知M在∠PF1O的角平分线上,∴四边形PF1OM为菱形,且边长为
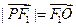 =c
=c∴
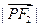 =2a+
=2a+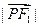 =2a+c,由第二定义=e即=e,∴+1=e且e>1
=2a+c,由第二定义=e即=e,∴+1=e且e>1∴e="2"
(2)由e=2,∴c=2a即b2=3a2,双曲线方程为 -=1
又N(,2)在双曲线上,∴-=1,∴a2=3∴双曲线的方程为-=1;
(3)由
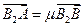 知AB过点B2,若AB⊥x轴,即AB的方程为x=3,此时AB1与BB1不垂直;设AB的方程为y=k(x-3)代入-=1得
知AB过点B2,若AB⊥x轴,即AB的方程为x=3,此时AB1与BB1不垂直;设AB的方程为y=k(x-3)代入-=1得(3k2-1)x2-18k2x+27k2-9="0"
由题知3k2-1≠0且△>0即k2> 且k2≠,
设交点A(x1,y1),B(x2,y2),
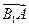 =(x1+3,y1),
=(x1+3,y1),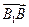 =(x2+3,y2),
=(x2+3,y2),∵
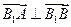 ,∴
,∴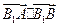 =0即x1x2+3(x1+x2)+9+y1y2=0
=0即x1x2+3(x1+x2)+9+y1y2=0 此时x1+x2=,x1·x2=9,
y1y2=k2(x1-3) (x2-3)=k2[x1x2-3(x1+x2)+9]= k2[18-]=-
∴9+3+9-=0,∴5 k2=1,∴k=±
∴AB的方程为y=±(x-3) .

练习册系列答案
相关题目
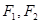 是双曲线
是双曲线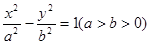 的左、右焦点,
的左、右焦点,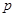 为双曲线左支上一点,若
为双曲线左支上一点,若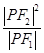 的最小值为
的最小值为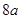 ,则该双曲线的离心率的取值范围是
,则该双曲线的离心率的取值范围是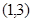
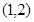
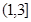
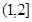
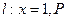 为该平面上一动点,作
为该平面上一动点,作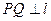 ,垂足为Q,且
,垂足为Q,且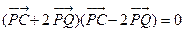 .
.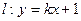 与(1)中的曲线交于不同的两点A、B,是否存在实数k,使得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由.
与(1)中的曲线交于不同的两点A、B,是否存在实数k,使得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由.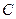 的中心在原点,对称轴为坐标轴,其一条渐近线方程是
的中心在原点,对称轴为坐标轴,其一条渐近线方程是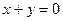 ,且双曲线
,且双曲线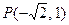 .
. 过点
过点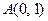 ,其方向向量为
,其方向向量为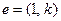
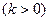 ,令向量
,令向量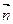 满足
满足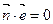 .双曲线
.双曲线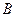 ,使得
,使得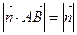 . 若存在,求出对应的
. 若存在,求出对应的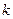 值和
值和
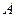 (1,0),点
(1,0),点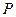 、Q在双曲线的右支上,点
、Q在双曲线的右支上,点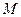 (
(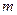 ,0)到直线
,0)到直线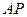 的距离为1.
的距离为1.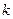 且有
且有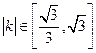 ,求实数
,求实数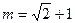 时,
时,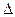
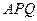 的内心恰好是点
的内心恰好是点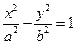 的右顶点,过点A且垂直于x轴的直线与双曲线的两条渐近线交于B、C两点,若△BOC为锐角三角形,则离心率的取值范围为________________.
的右顶点,过点A且垂直于x轴的直线与双曲线的两条渐近线交于B、C两点,若△BOC为锐角三角形,则离心率的取值范围为________________.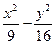 =1的两焦点为F1、F2,点P在双曲线上,且直线PF1、PF2倾斜角之差为
=1的两焦点为F1、F2,点P在双曲线上,且直线PF1、PF2倾斜角之差为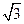 ,则△PF1F2的面积为( )
,则△PF1F2的面积为( )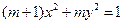 表示焦点在
表示焦点在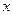 轴上的双曲线,则实数
轴上的双曲线,则实数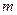 的取值范围是 .
的取值范围是 .