Question

在三棱锥SABC中，底面是边长为2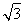的正三角形，点S在底面ABC上的射影O恰是AC的中点，侧棱SB和底面成45°角．

(1)若D为侧棱SB上一点，当为何值时，CD⊥AB；

(2)求二面角S-BC-A的余弦值大小．

 

Answer 1

（1）（2）

【解析】以O点为原点，OB为x轴，OC为y轴，OS为z轴建立空间直角坐标系O-xyz.

由题意知∠SBO＝45°，SO＝3.O(0，0，0)，C(0，，0)，A(0，－，0)，S(0，0，3)，B(3，0，0)．

(1)设＝λ(0≤λ≤1)，则＝(1＋λ)＋λ＝(3(1＋λ)，0，3λ)，

所以＝(3(1－λ)，－，3λ)．

因为＝(3，，0)，CD⊥AB，所以·＝9(1－λ)－3＝0，解得λ＝.

故时，CD⊥AB.

(2)平面ACB的法向量为n1＝(0，0，1)，设平面SBC的法向量n2＝(x，y，z)，则n2·＝0，n2·＝0，则解得取n2＝(1，，1)，

所以cos〈n1，n2〉＝＝.

又显然所求二面角的平面角为锐角，故所求二面角的余弦值的大小为.