题目内容
三棱锥S-ABC中,侧棱SA,SB,SC两两垂直,△SAB,△SBC,△SAC面积分别为1,
,3,则此三棱锥外接球表面积为
| 3 | 2 |
14π
14π
.分析:根据三角形面积公式,解方程组得SA=2,SB=1,SC=3,进而算出以SA、SB、SC为长、宽、高的长方体的对角线长为
,从而得到三棱锥外接球R=
,最后用球的表面积公式,可得此三棱锥外接球表面积.
| 14 |
| ||
| 2 |
解答:解:设SA=x,SB=y,SC=z,则
因为△SAB,△SBC,△SAC都是以S为直角顶点的直角三角形,得
解之得:x=2,y=1,z=3即SA=2,SB=1,SC=3,
∵侧棱SA,SB,SC两两垂直,
∴以SA、SB、SC为过同一顶点的3条棱作长方体,该长方体的对角线长为
=
,恰好等于三棱锥外接球的直径
由此可得外接球的半径R=
得此三棱锥外接球表面积为S=4πR2=14π
故答案为:14π
因为△SAB,△SBC,△SAC都是以S为直角顶点的直角三角形,得
|
解之得:x=2,y=1,z=3即SA=2,SB=1,SC=3,
∵侧棱SA,SB,SC两两垂直,
∴以SA、SB、SC为过同一顶点的3条棱作长方体,该长方体的对角线长为
| SA2+SB2+SC2 |
| 14 |
由此可得外接球的半径R=
| ||
| 2 |
故答案为:14π
点评:本题给出特殊三棱锥,求它的外接球表面积,着重考查了空间垂直关系的性质和多面体的外接球等知识,属于中档题.

练习册系列答案
相关题目
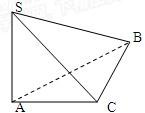 如图在三棱锥S-ABC中∠ACB=90°,SA⊥面ABC,AC=2,
如图在三棱锥S-ABC中∠ACB=90°,SA⊥面ABC,AC=2,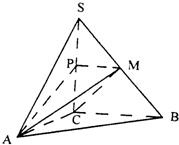 如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°.
如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°. 如图,在三棱锥S-ABC中,△ABC是边长为8的正三角形,
如图,在三棱锥S-ABC中,△ABC是边长为8的正三角形, 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2