题目内容
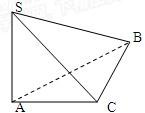 如图在三棱锥S-ABC中∠ACB=90°,SA⊥面ABC,AC=2,BC=
如图在三棱锥S-ABC中∠ACB=90°,SA⊥面ABC,AC=2,BC=| 13 |
| 29 |
(1)证明SC⊥BC.
(2)求侧面SBC与底面ABC所成二面角的大小.
分析:(1)因为SA⊥面ABC,AC为SC在面ABC内的射影,由三垂线定理可直接得证.
(2)由题意可直接找出侧面SBC与底面ABC所成二面角的平面角是∠SCA,在直角三角形中求解即可.
(2)由题意可直接找出侧面SBC与底面ABC所成二面角的平面角是∠SCA,在直角三角形中求解即可.
解答:解:(1)∵∠SAB=∠SCA=90°
∴SA⊥AB SA⊥AC AB∩AC=A
∴SA⊥面ABC
由于∠ACB=90° 即BC⊥AC
由三重线定理SC⊥BC
(2)∵BC⊥AC BC⊥SC
∴∠SCA是侧面SBC与底面ABC所成二面角的平面角
在Rt△SCB中,由于BC=
,SB=
SC=4
在Rt△SAC中,由于AC=2 SC=4
∴COS∠SCA=
=
∴∠SCA=60°
即侧面SBC与底面ABC形成的二面角的大小为60°.
∴SA⊥AB SA⊥AC AB∩AC=A
∴SA⊥面ABC
由于∠ACB=90° 即BC⊥AC
由三重线定理SC⊥BC
(2)∵BC⊥AC BC⊥SC
∴∠SCA是侧面SBC与底面ABC所成二面角的平面角
在Rt△SCB中,由于BC=
| 13 |
| 29 |
在Rt△SAC中,由于AC=2 SC=4
∴COS∠SCA=
| AC |
| SC |
| 1 |
| 2 |
∴∠SCA=60°
即侧面SBC与底面ABC形成的二面角的大小为60°.
点评:本题考查两条直线垂直的证明、三垂线定理的应用、二面角的求解,考查逻辑推理能力和运算能力.

练习册系列答案
相关题目
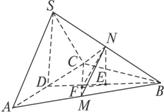
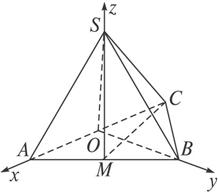
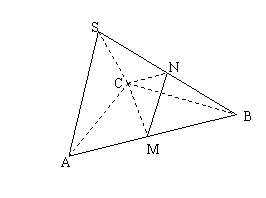 SA=SC=
SA=SC=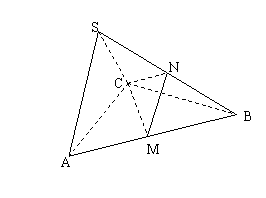 SA=SC=
SA=SC=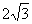 ,M,N分别为AB,SB的中点。
,M,N分别为AB,SB的中点。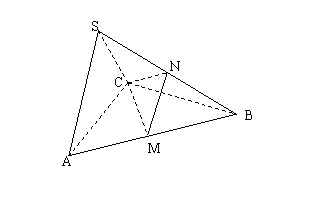 (Ⅲ)求点B到平面CMN的距离。
(Ⅲ)求点B到平面CMN的距离。