题目内容
将函数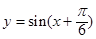 的图象上图象上各点的横坐标扩大到原来的2倍(纵坐标不变),再将所得函数图象上所有的点向左平行移动
的图象上图象上各点的横坐标扩大到原来的2倍(纵坐标不变),再将所得函数图象上所有的点向左平行移动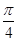 个单位长度,则所得到的图象的解析式为( )
个单位长度,则所得到的图象的解析式为( )
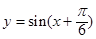 的图象上图象上各点的横坐标扩大到原来的2倍(纵坐标不变),再将所得函数图象上所有的点向左平行移动
的图象上图象上各点的横坐标扩大到原来的2倍(纵坐标不变),再将所得函数图象上所有的点向左平行移动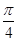 个单位长度,则所得到的图象的解析式为( )
个单位长度,则所得到的图象的解析式为( )A. (x∈R) (x∈R) | B.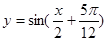 (x∈R) (x∈R) |
C.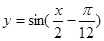 (x∈R) (x∈R) | D.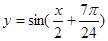 (x∈R) (x∈R) |
D
分析:首先根据将原函数的图象上所有点的横坐标伸长到原来的2倍,得到函数y=sin(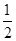 x+
x+ 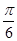 ),再根据左加右减的平移原则即可得到函数解析式.
),再根据左加右减的平移原则即可得到函数解析式.
解答:解:将函数y=sin(x+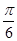 )图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),即周期变为原来的两倍,
)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),即周期变为原来的两倍,
可得函数解析式为:y=sin(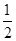 x+
x+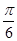 ),
),
再将所得的函数图象向左平移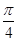 个单位,可得其解析式为:y=sin[
个单位,可得其解析式为:y=sin[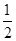 (x+
(x+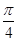 )+
)+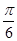 ]=sin(
]=sin(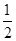 x+
x+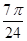 ),
),
故选D.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,着重考查三角函数的平移原则(左加右减上加下减),考查计算能力,属于中档题.
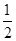 x+
x+ 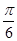 ),再根据左加右减的平移原则即可得到函数解析式.
),再根据左加右减的平移原则即可得到函数解析式.解答:解:将函数y=sin(x+
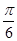 )图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),即周期变为原来的两倍,
)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),即周期变为原来的两倍,可得函数解析式为:y=sin(
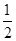 x+
x+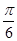 ),
),再将所得的函数图象向左平移
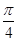 个单位,可得其解析式为:y=sin[
个单位,可得其解析式为:y=sin[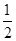 (x+
(x+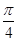 )+
)+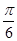 ]=sin(
]=sin(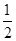 x+
x+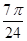 ),
),故选D.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,着重考查三角函数的平移原则(左加右减上加下减),考查计算能力,属于中档题.

练习册系列答案
相关题目
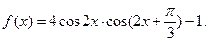
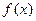 的最小值及此时x的取值集合;
的最小值及此时x的取值集合;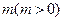 个单位后所得图象关于y轴对称,求m的最小值。
个单位后所得图象关于y轴对称,求m的最小值。
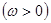 的图象与
的图象与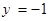 的图象的两相邻交点间的距离为π,要得到y=
的图象的两相邻交点间的距离为π,要得到y=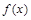 的图象,只需把y=sin
的图象,只需把y=sin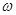 x的图象( )
x的图象( )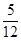 π个单位
π个单位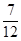 π个单位
π个单位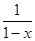 的图象与函数y=2sinπx(-2≤x≤4)的图象所有交点的横坐标之
的图象与函数y=2sinπx(-2≤x≤4)的图象所有交点的横坐标之 x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函
x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函
 的最小正周期为
的最小正周期为 .
. 的值; (Ⅱ)求函数
的值; (Ⅱ)求函数 的单调递增区间及其图象的对称轴方程.
的单调递增区间及其图象的对称轴方程.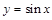 的图像,只需将函数
的图像,只需将函数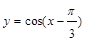 的图像( )
的图像( )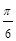 个单位
个单位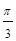 个单位
个单位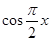 的最小值、最大值分别是( )
的最小值、最大值分别是( )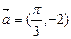 平移后,得到的图象的表达式为
平移后,得到的图象的表达式为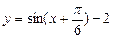 ,则原函数的解析式为
,则原函数的解析式为