题目内容
某公司在“2010年上海世博会知识宣传”活动中进行抽奖游戏.抽奖规则是:在一个盒子中装有6张大小相同的精美卡片,其中3张印有“世博会会徽”图案,3张印有“世博会吉祥物海宝”图案.现每一次从盒子里无放回的随机抽取一张卡片,抽到印有海宝图案的卡片就中奖且游戏结束.(Ⅰ)求最多抽取两次卡片游戏就结束的概率;
(Ⅱ)用X表示游戏结束时所抽取卡片的次数,求X的分布列和数学期望.
分析:(1)由题意知最多摸两次中奖包括第一次模卡中奖和第二次摸卡中奖,这两种结果是互斥的,做出第一次摸卡中奖的概率和第二次摸卡中奖的概率,得到结果.
(2)X表示摸卡的次数,现从盒子里无放回的摸取卡片,找出印有“海宝”图案的卡片表示中奖且停止摸卡,则变量的最大值是4,结合变量对应的事件做出分布列和期望.
(2)X表示摸卡的次数,现从盒子里无放回的摸取卡片,找出印有“海宝”图案的卡片表示中奖且停止摸卡,则变量的最大值是4,结合变量对应的事件做出分布列和期望.
解答:解:(1)由题意知最多摸两次中奖包括第一次模卡中奖和第二次摸卡中奖,
这两种结果是互斥的,
第一次摸卡中奖的概率为 P1=
=
第二次摸卡中奖的概率为 P2=
=
则最多摸两次中奖的概率为 P=P1+P2=
(2)由题意,摸卡次数X的取值为:1,2,3,4
P(X=1)=P1=
;P(X=2)=P2=
P(X=3)=
=
P(X=4)=
=
∴则ξ的分布列为:
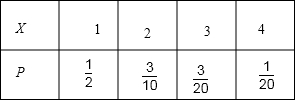
∴EX=1×
+2×
+3×
+4×
=
这两种结果是互斥的,
第一次摸卡中奖的概率为 P1=
| ||
|
| 1 |
| 2 |
第二次摸卡中奖的概率为 P2=
| ||||
|
| 3 |
| 10 |
则最多摸两次中奖的概率为 P=P1+P2=
| 4 |
| 5 |
(2)由题意,摸卡次数X的取值为:1,2,3,4
P(X=1)=P1=
| 1 |
| 2 |
| 3 |
| 10 |
P(X=3)=
| ||||
|
| 3 |
| 20 |
P(X=4)=
| ||
|
| 1 |
| 20 |
∴则ξ的分布列为:

∴EX=1×
| 1 |
| 2 |
| 3 |
| 10 |
| 3 |
| 20 |
| 1 |
| 20 |
| 7 |
| 4 |
点评:题考查求离散型随机变量的分布列和期望,这种问题是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,只要注意解题规范,就可以得分.

练习册系列答案
相关题目
 表示摸卡的次数,求
表示摸卡的次数,求