题目内容
在△ABC中,已知内角A、B、C所对的边分别为a、b、c,且a2+b2=c2+ab.
(1)若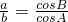 ,且c=2,求△ABC的面积;
,且c=2,求△ABC的面积;
(2)已知向量 =(sinA,cosA),
=(sinA,cosA), =(cosB,-sinB),求|
=(cosB,-sinB),求|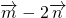 |的取值范围.
|的取值范围.
解析:(1)在△ABC中,∵a2+b2=c2+ab,即c2=a2+b2-ab,
∴cosC= =
= ,结合C∈(0,π)得C=
,结合C∈(0,π)得C=
又∵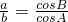 ,可得
,可得 ,
,
∴sinAcosA=sinBcosB,即sin2A=sin2B,
∴A=B或
当 时,与C=
时,与C= 矛盾,故A=B,可得△ABC是等边三角形.
矛盾,故A=B,可得△ABC是等边三角形.
∵c=2,∴△ABC的面积 …(6分)
…(6分)
(2)∵向量 =(sinA,cosA),
=(sinA,cosA), =(cosB,-),
=(cosB,-),
∴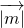 =1,
=1,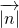 =1,
=1, •
• =sinAcosB-cosAsinB=sin(A-B)
=sinAcosB-cosAsinB=sin(A-B)
因此,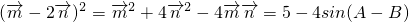
∵A+B= ,得A=
,得A= -B
-B
∴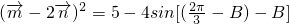 =
=
∵B∈(0, ),得
),得 -2B∈(-
-2B∈(- ,
, )…(10分)
)…(10分)
∴当 -2B=-
-2B=- 时,
时, 有最小值-1,此时
有最小值-1,此时 有最大值9;
有最大值9;
当 -2B=
-2B= 时,
时, 有最大值1,此时
有最大值1,此时 有最小值1.
有最小值1.
可得 ,开方得
,开方得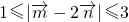
故|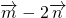 |的取值范围[1,3]. …(12分)
|的取值范围[1,3]. …(12分)
分析:(1)根据余弦定理结合题中平方关系的等式,算出cosC= ,从而得出C=
,从而得出C= .再由正弦定理结合题中比例式,化简可得sin2A=sin2B,因此△ABC是等边三角形,不难得出△ABC的面积.
.再由正弦定理结合题中比例式,化简可得sin2A=sin2B,因此△ABC是等边三角形,不难得出△ABC的面积.
(2)首先计算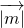 =
=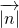 =1,且
=1,且 •
• =sin(A-B),代入
=sin(A-B),代入 表达式并化简,得
表达式并化简,得 =
= ,根据角B的取值范围结合正弦函数的单调性,可得
,根据角B的取值范围结合正弦函数的单调性,可得 ,两边开方即得|
,两边开方即得|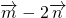 |的取值范围.
|的取值范围.
点评:本题是一道三角函数综合题,着重考查了平面向量数量积的坐标表示、模的公式,以及运用正余弦定理解三角形等知识,属于中档题.
∴cosC=
 =
= ,结合C∈(0,π)得C=
,结合C∈(0,π)得C=
又∵
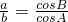 ,可得
,可得 ,
,∴sinAcosA=sinBcosB,即sin2A=sin2B,
∴A=B或

当
 时,与C=
时,与C= 矛盾,故A=B,可得△ABC是等边三角形.
矛盾,故A=B,可得△ABC是等边三角形.∵c=2,∴△ABC的面积
 …(6分)
…(6分)(2)∵向量
 =(sinA,cosA),
=(sinA,cosA), =(cosB,-),
=(cosB,-),∴
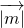 =1,
=1,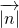 =1,
=1, •
• =sinAcosB-cosAsinB=sin(A-B)
=sinAcosB-cosAsinB=sin(A-B)因此,
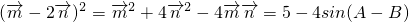
∵A+B=
 ,得A=
,得A= -B
-B ∴
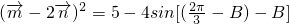 =
=
∵B∈(0,
 ),得
),得 -2B∈(-
-2B∈(- ,
, )…(10分)
)…(10分)∴当
 -2B=-
-2B=- 时,
时, 有最小值-1,此时
有最小值-1,此时 有最大值9;
有最大值9;当
 -2B=
-2B= 时,
时, 有最大值1,此时
有最大值1,此时 有最小值1.
有最小值1.可得
 ,开方得
,开方得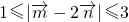
故|
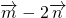 |的取值范围[1,3]. …(12分)
|的取值范围[1,3]. …(12分)分析:(1)根据余弦定理结合题中平方关系的等式,算出cosC=
 ,从而得出C=
,从而得出C= .再由正弦定理结合题中比例式,化简可得sin2A=sin2B,因此△ABC是等边三角形,不难得出△ABC的面积.
.再由正弦定理结合题中比例式,化简可得sin2A=sin2B,因此△ABC是等边三角形,不难得出△ABC的面积.(2)首先计算
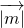 =
=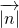 =1,且
=1,且 •
• =sin(A-B),代入
=sin(A-B),代入 表达式并化简,得
表达式并化简,得 =
= ,根据角B的取值范围结合正弦函数的单调性,可得
,根据角B的取值范围结合正弦函数的单调性,可得 ,两边开方即得|
,两边开方即得|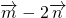 |的取值范围.
|的取值范围.点评:本题是一道三角函数综合题,着重考查了平面向量数量积的坐标表示、模的公式,以及运用正余弦定理解三角形等知识,属于中档题.

练习册系列答案
相关题目





