题目内容
（2011•江苏模拟）在△ABC中，已知
•
=9，sinB=cosAsinC，面积S△ABC=6．
（Ⅰ）求△ABC的三边的长；
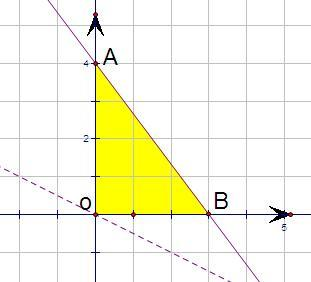
（Ⅱ）设P是△ABC（含边界）内一点，P到三边AC，BC，AB的距离分别为x，y和z，求x+y+z的取值范围．
| AB |
| AC |
（Ⅰ）求△ABC的三边的长；
（Ⅱ）设P是△ABC（含边界）内一点，P到三边AC，BC，AB的距离分别为x，y和z，求x+y+z的取值范围．
分析：（1）设三边分别为a，b，c，利用正弦定理和余弦定理将题中条件角的关系转化成边的关系，得到直角三角形ABC，再结合向量条件利用三角形面积公式即可求出三边长．
（2）欲求x+y+z的取值范围，利用坐标法，将三角形ABC放置在直角坐标系中，通过点到直线的距离将求x+y+z的范围转化为x+y+z=
+
(2x+y)，最后结合线性规划的思想方法求出范围即可．
（2）欲求x+y+z的取值范围，利用坐标法，将三角形ABC放置在直角坐标系中，通过点到直线的距离将求x+y+z的范围转化为x+y+z=
| 12 |
| 5 |
| 1 |
| 5 |
解答：解：设AB=c，AC=b，BC=a．
（Ⅰ）
⇒tanA=
，sinA=
，cosA=
，
bc=15，
=cosA⇒
=
，
由
⇒
，
用余弦定理得：a=4…（7分）
（Ⅱ）2S△ABC=3x+4y+5z=12⇒x+y+z=
+
(2x+y)
设t=2x+y，
由线性规划得0≤t≤8．
∴
≤x+y+z≤4．…（13分）
（Ⅰ）
|
| 4 |
| 3 |
| 4 |
| 5 |
| 3 |
| 5 |
bc=15，
| sinB |
| sinC |
| b |
| c |
| 3 |
| 5 |
由
|
|
用余弦定理得：a=4…（7分）
（Ⅱ）2S△ABC=3x+4y+5z=12⇒x+y+z=
| 12 |
| 5 |
| 1 |
| 5 |
设t=2x+y，
|
∴
| 12 |
| 5 |
点评：本题主要考查了解三角形中正弦定理、余弦定理、平面向量数量积的运算、简单线性规划思想方法的应用，属于中档题．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
