题目内容
在△ABC中，已知
•
=9．sinB=cosAsinC，面积S△ABC=6，
（1）求△ABC的三边的长；
（2）设P是△ABC（含边界）内的一点，P到三边AC、BC、AB的距离分别是x、y、z．
①写出x、y、z．所满足的等量关系；
②利用线性规划相关知识求出x+y+z的取值范围．
| AB |
| AC |
（1）求△ABC的三边的长；
（2）设P是△ABC（含边界）内的一点，P到三边AC、BC、AB的距离分别是x、y、z．
①写出x、y、z．所满足的等量关系；
②利用线性规划相关知识求出x+y+z的取值范围．
分析：（1）设△ABC中的三边分别为a、b、c，由三角形内角和化简sinB=cosAsinC，算出C=
．由此化简
•
=9，得到b2=9，解出b=3，代入三角形面积公式算出a=4，最后由勾股定理即可算出c的长；
（2）①由三角形面积公式将△ABC的面积分为三块计算，化简得3x+4y+5z=12，即为x、y、z．所满足的等量关系；
②由①化简出x+y+z=
+
(2x+y)，设目标函数t=2x+y，并根据不等式画出如图可行域，利用直线平移法解出0≤t≤8，从而可得x+y+z的取值范围．
| π |
| 2 |
| AB |
| AC |
（2）①由三角形面积公式将△ABC的面积分为三块计算，化简得3x+4y+5z=12，即为x、y、z．所满足的等量关系；
②由①化简出x+y+z=
| 12 |
| 5 |
| 1 |
| 5 |
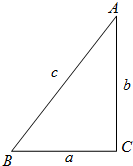
解答：解：（1）设△ABC中角ABC所对边分别为a、b、c
由sinB=cosAsinC，得sin（A+C）=cosAsinC
∴sinAcosC=0，可得C=
又∵
•
=9，得bccosA=9
∴结合ccosA=b，有b2=9，可得b=3．
∵S△ABC=
a•b=6，∴a=4
结合c2=a2+b2得c=5
即△ABC的三边长a=4，b=3，c=5…（4分）
（2）①S△PAC+S△PBC+S△PAB=S△ABC，可得
•3x+
•4y+
•5z=6，故3x+4y+5z=12…（8分）
②x+y+z=x+y+
(12-3x-4y)=
+
(2x+y)
令t=2x+y依题意有
…（10分）
画出可行域如图
可知当x=0，y=0时tmin=0
当x=4，y=0时，tmax=8，即0≤t≤8
故x+y+z=
+
t的取值范围为[
，4]…（13分）
由sinB=cosAsinC，得sin（A+C）=cosAsinC∴sinAcosC=0，可得C=
| π |
| 2 |
又∵
| AB |
| AC |
∴结合ccosA=b，有b2=9，可得b=3．
∵S△ABC=
| 1 |
| 2 |
结合c2=a2+b2得c=5
即△ABC的三边长a=4，b=3，c=5…（4分）
（2）①S△PAC+S△PBC+S△PAB=S△ABC，可得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②x+y+z=x+y+
| 1 |
| 5 |
| 12 |
| 5 |
| 1 |
| 5 |
令t=2x+y依题意有
|
画出可行域如图
可知当x=0，y=0时tmin=0
当x=4，y=0时，tmax=8，即0≤t≤8
故x+y+z=
| 12 |
| 5 |
| 1 |
| 5 |
| 12 |
| 5 |
点评：本题着重考查了向量的数量积、三角形的面积公式、勾股定理的知识，考查了简单的线性规则的知识，属于中档题．请同学们注意解题过程中转化化归、数形结合和方程思想的运用．
练习册系列答案
相关题目