题目内容
6.在平面直角坐标系xOy中,椭圆C方程为$\left\{\begin{array}{l}x=5cosφ\\ y=3sinφ\end{array}\right.(φ$为参数),求过椭圆的右焦点,且与直线$\left\{\begin{array}{l}x=4-2t\\ y=3-t\end{array}\right.(t$为参数)平行的直线l的普通方程.分析 利用cos2φ+sin2φ=1可把椭圆C方程为$\left\{\begin{array}{l}x=5cosφ\\ y=3sinφ\end{array}\right.(φ$为参数),化为普通方程.可得$c=\sqrt{{a}^{2}-{b}^{2}}$.直线$\left\{\begin{array}{l}x=4-2t\\ y=3-t\end{array}\right.(t$为参数)化为普通方程:x-2y+2=0,可设与上述平行的直线l的普通方程为x-2y+m=0,把右焦点坐标代入即可得出.
解答 解:椭圆C方程为$\left\{\begin{array}{l}x=5cosφ\\ y=3sinφ\end{array}\right.(φ$为参数),化为普通方程:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1$.
∴$c=\sqrt{25-9}$=4.
可得椭圆的右焦点为F(4,0),
直线$\left\{\begin{array}{l}x=4-2t\\ y=3-t\end{array}\right.(t$为参数)化为普通方程:x-2y+2=0,
可设与上述平行的直线l的普通方程为x-2y+m=0.
把F代入可得:4-0+m=0,解得m=-4.
于是所求直线方程为x-2y+4=0.
点评 本题考查了椭圆的参数方程化为普通方程、椭圆的标准方程及其性质、相互平行的直线斜率之间的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
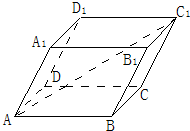 已知平行六面体,AB=AD=AA1=1,∠BAD=∠BAA1=∠DAA1=60°,求|$\overrightarrow{A{C}_{1}}$|.
已知平行六面体,AB=AD=AA1=1,∠BAD=∠BAA1=∠DAA1=60°,求|$\overrightarrow{A{C}_{1}}$|.