题目内容
已知曲线C:xy-4x+4=0,数列{an}的首项a1=4,且当n≥2时,点(an-1,an)恒在曲线C上,数列{bn}满足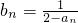 .
.
(1)试判断数列{bn}是否是等差数列?并说明理由;
(2)求数列{an}和{bn}的通项公式;
(3)设数列{cn}满足anbn2cn=1,试比较数列{cn}的前n项和Sn与2的大小.
解:(1)∵当n≥2时,点(an-1,an)恒在曲线C上
∴an-1an-4an-1+4=0(1分)
由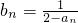 得
得
当n≥2时,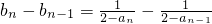
=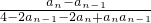
=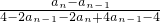
= (4分)
(4分)
∴数列{bn}是公差为 的等差数列;(5分)
的等差数列;(5分)
(2)∵a1=4,∴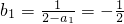
∴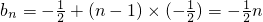 (7分)
(7分)
由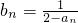 得
得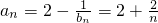 (9分)
(9分)
(3)∵anbn2cn=1
∴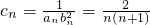 =
=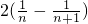 (10分)
(10分)
∴Sn=c1+c2++cn=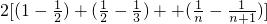
=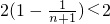 .(12分)
.(12分)
分析:本题以点(an-1,an)恒在曲线C:xy-4x+4=0上为情景,考查等差数列的证明、求数列的通项公式、求数列的前n项和等数列知识和研究方法;
(1)根据点(an-1,an)在曲线C上,将其代入方程可得:an-1an-4an-1+4=0,由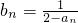 相邻两项作差得到-
相邻两项作差得到- ,所以数列{bn}是等差数列
,所以数列{bn}是等差数列
(2)由(1)知数列{bn}是等差数列,首项和公差易得,所以数列{bn}的通项公式可求,再根据两个数列的关系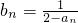 ,数列{an}的通项公式可直接获得;
,数列{an}的通项公式可直接获得;
(3)根据数列{cn}满足anbn2cn=1,由(2)可得数列{cn}的通项公式,前n项和可由“裂项法”求得,与2的大小比较易得.
点评:本题综合性强,知识联系广泛,涉及了数列的证明、通项公式、求和公式等,但解题思路清晰、方向明确;
注意在数列{bn}是否是等差数列的判断时,运用bn-bn-1容易进行判断,在(3)得到Sn=c1+c2++cn=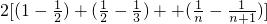 =
= 后,会变形为
后,会变形为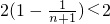 易得.
易得.
∴an-1an-4an-1+4=0(1分)
由
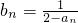 得
得当n≥2时,
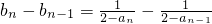
=
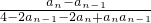
=
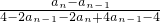
=
 (4分)
(4分)∴数列{bn}是公差为
 的等差数列;(5分)
的等差数列;(5分)(2)∵a1=4,∴
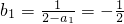
∴
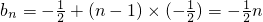 (7分)
(7分)由
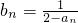 得
得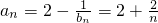 (9分)
(9分)(3)∵anbn2cn=1
∴
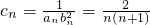 =
=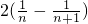 (10分)
(10分)∴Sn=c1+c2++cn=
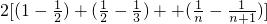
=
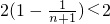 .(12分)
.(12分)分析:本题以点(an-1,an)恒在曲线C:xy-4x+4=0上为情景,考查等差数列的证明、求数列的通项公式、求数列的前n项和等数列知识和研究方法;
(1)根据点(an-1,an)在曲线C上,将其代入方程可得:an-1an-4an-1+4=0,由
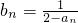 相邻两项作差得到-
相邻两项作差得到- ,所以数列{bn}是等差数列
,所以数列{bn}是等差数列(2)由(1)知数列{bn}是等差数列,首项和公差易得,所以数列{bn}的通项公式可求,再根据两个数列的关系
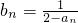 ,数列{an}的通项公式可直接获得;
,数列{an}的通项公式可直接获得;(3)根据数列{cn}满足anbn2cn=1,由(2)可得数列{cn}的通项公式,前n项和可由“裂项法”求得,与2的大小比较易得.
点评:本题综合性强,知识联系广泛,涉及了数列的证明、通项公式、求和公式等,但解题思路清晰、方向明确;
注意在数列{bn}是否是等差数列的判断时,运用bn-bn-1容易进行判断,在(3)得到Sn=c1+c2++cn=
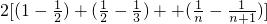 =
= 后,会变形为
后,会变形为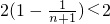 易得.
易得. 
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
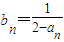 .
.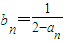 .
.