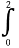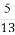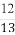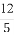题目内容
已知函数f(x)=x3-3x.
(1)求函数f(x)的单调区间.
(2)求函数f(x)在区间[-3,2]上的最值.
(1) (-1,1) (2) 当x=-3时, 最小值为-18。当x=-1或2时, 最大值为2
【解析】(1)∵f(x)=x3-3x,
∴f'(x)=3x2-3=3(x+1)(x-1).
令f'(x)=0,得x=-1或x=1.
若x∈(-∞,-1)∪(1,+∞),则f'(x)>0,
故f(x)的单调增区间为(-∞,-1),(1,+∞),
若x∈(-1,1),则f'(x)<0,故f(x)的单调减区间为(-1,1).
(2)∵f(-3)=-18,f(-1)=2,f(1)=-2,f(2)=2,
∴当x=-3时,f(x)在区间[-3,2]取到最小值为-18.
∴当x=-1或2时,f(x)在区间[-3,2]取到最大值为2.

练习册系列答案
相关题目