题目内容
若三棱锥P-ABC的三条侧棱与底面所成的角都相等，则点P在底面ABC上的射影一定是△ABC的（ ）
分析：设点P在底面ABC上的射影点为0，由∠PAO=∠PBO=∠PCO，PO=PO=PO，∠POA=∠POB=∠POC=90°，先证明△PAO≌△PBO≌△PCO，从而得到AO=BO=CO，由此可知O是△ABC的外心．
解答：解：设点P在底面ABC上的射影点为0，
∵∠PAO=∠PBO=∠PCO，
PO=PO=PO，
∠POA=∠POB=∠POC=90°，
∴△PAO≌△PBO≌△PCO，
∴AO=BO=CO
∴O是△ABC的外心．
故选A．
∵∠PAO=∠PBO=∠PCO，
PO=PO=PO，
∠POA=∠POB=∠POC=90°，
∴△PAO≌△PBO≌△PCO，
∴AO=BO=CO
∴O是△ABC的外心．
故选A．
点评：三角形的三边垂直平分线的交点叫三角形的外心，它到三角形三个项点的距离相等；三角形的三条角平分线的交点叫三角形的内心，它到三角形三边的距离相等；三角形的三边中线的交叫叫重心，它到顶点的距离等于它到对边距离的二倍；三角形三条高的交点叫垂心．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
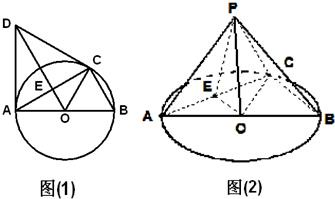如图（1），C是直径AB=2的⊙O上一点，AD为⊙O的切线，A为切点，△ACD为等边三角形，连接DO交AC于E，以AC为折痕将△ACD翻折到图（2）的△ACP位置．
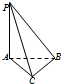已知如图在三棱锥P-ABC中，PA⊥平面ABC，AC⊥BC，PA=AC=BC=1，若三棱锥P-ABC的四个顶点都在某一个球面上，则该球的表面积为（ ）