题目内容
若三棱锥P-ABC的底面ABC是正三角形，则三个侧面的面积相等是三棱锥P-ABC是正三棱锥的（ ）
分析：通过三棱锥P-ABC的底面ABC是正三角形，三个侧面的面积相等，推出三棱锥P-ABC是正三棱锥，通过三棱锥P-ABC是正三棱锥判断三棱锥P-ABC的底面ABC是正三角形，则三个侧面的面积相等，得到结果．
解答：解：因为三棱锥P-ABC的底面ABC是正三角形，三个侧面的面积相等，
说明三个侧面是等腰三角形，所以三棱锥P-ABC是正三棱锥；
通过三棱锥P-ABC是正三棱锥，由正三棱锥的定义可知三棱锥P-ABC的底面ABC是正三角形，三个侧面全等，所以三个侧面的面积相等；
所以三棱锥P-ABC的底面ABC是正三角形，则三个侧面的面积相等是三棱锥P-ABC是正三棱锥的充要条件，
故选C．
说明三个侧面是等腰三角形，所以三棱锥P-ABC是正三棱锥；
通过三棱锥P-ABC是正三棱锥，由正三棱锥的定义可知三棱锥P-ABC的底面ABC是正三角形，三个侧面全等，所以三个侧面的面积相等；
所以三棱锥P-ABC的底面ABC是正三角形，则三个侧面的面积相等是三棱锥P-ABC是正三棱锥的充要条件，
故选C．
点评：本题考查充要条件的应用，正三棱锥的定义的理解，考查基本知识的应用．
练习册系列答案
相关题目
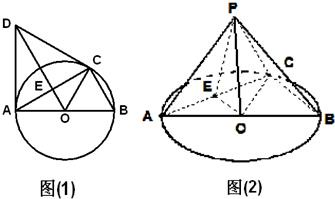如图（1），C是直径AB=2的⊙O上一点，AD为⊙O的切线，A为切点，△ACD为等边三角形，连接DO交AC于E，以AC为折痕将△ACD翻折到图（2）的△ACP位置．
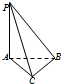已知如图在三棱锥P-ABC中，PA⊥平面ABC，AC⊥BC，PA=AC=BC=1，若三棱锥P-ABC的四个顶点都在某一个球面上，则该球的表面积为（ ）