题目内容
在平面直角坐标系中，设点P（x，y），定义[OP]=|x|+|y|，其中O为坐标原点，则满足[OP]=1的点P的轨迹围成的图形的面积为分析：由已知中在平面直角坐标系中，设点P（x，y），定义[OP]=|x|+|y|，则满足[OP]=1的点P的坐标满足|x|+|y|=1，画出满足条件的图形，即可得到点P的轨迹围成的图形的面积．
解答：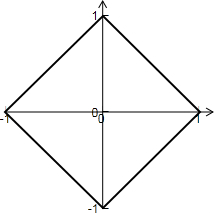
解：∵点P（x，y）中有[OP]=|x|+|y|，
当[OP]=1时，即|x|+|y|=1
满足条件的图形如下图所示：
由图可知，满足条件的图形是一个边长为
的正方形
故其面积S=2
故答案为：2
解：∵点P（x，y）中有[OP]=|x|+|y|，当[OP]=1时，即|x|+|y|=1
满足条件的图形如下图所示：
由图可知，满足条件的图形是一个边长为
| 2 |
故其面积S=2
故答案为：2
点评：本题考查的知识点是直线和圆方程的应用，其中根据绝对值的意义画出满足|x|+|y|=1的图形，是解答本题的关键．
练习册系列答案
名师点拨卷系列答案
相关题目