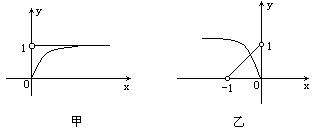题目内容

已知函数f(x)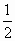＝lg(kx)，g(x)＝lg(x＋1)．

(1)求f(x)－g(x)的定义域；

(2)若方程f(x)＝g(x)有且仅有一个实数解，求实数k的取值范围．

答案：
解析：

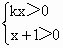　　(1)所以若k＞0，则定义域为x＞0；若k＜0，则定义域为－1＜x＜0．

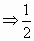　　(2)f(x)＝g(x)lg(kx)＝lg(x＋1)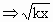＝x＋1，此方程在定义域内有且只有一解，令y1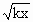＝(y1＞0)，y2＝x＋1(y2＞0)；当k＞0时，x＞0，则y1、y2的图像如图甲所示．令Δ＝0，解得k＝4或k＝0(舍去)，∴k＝4时，方程在定义域内有一解；又k＜0时，－1＜x＜0，此时y1、y2的图像如图乙所示，方程必有且只有一个实数解．综合知k＜0，或k＝4时，方程f(x)＝g(x)有且只有一个实数解．


练习册系列答案
相关题目

已知函数f(x)＝ax2－2x＋1，g(x)＝ln(x＋1)．

(1)求函数y＝g(x)－x在[0,1]上的最小值；

(2)当a≥时，函数t(x)＝f(x)＋g(x)的图像记为曲线C，曲线C在点(0,1)处的切线为l，是否存在a使l与曲线C有且仅有一个公共点？若存在，求出所有a的值；否则，说明理由．

(3)当x≥0时，g(x)≥－f(x)＋恒成立，求a的取值范围．

已知函数f(x)＝x3＋x－16，

(1)求曲线y＝f(x)在点(2，－6)处的切线的方程；

(2)直线l为曲线y＝f(x)的切线，且经过原点，求直线l的方程及切点坐标；

 

已知函数f(x)＝x3－3x及y＝f(x)上一点P(1，－2)，过点P作直线l.

(1)求使直线l和y＝f(x)相切且以P为切点的直线方程；

(2)求使直线l和y＝f(x)相切且切点异于P的直线方程．

 

已知函数f(x)＝x3＋ax2＋bx＋c，曲线y＝f(x)在x＝1处的切线为l：3x－y＋1＝0，当x＝时，y＝f(x)有极值．

(1)求a、b、c的值；

(2)求y＝f(x)在[－3,1]上的最大值和最小值．

 

已知函数f(x)＝x3－2x2＋ax(x∈R，a∈R)，在曲线y＝f(x)的所有切线中，有且仅有一条切线l与直线y＝x垂直．

(1)求a的值和切线l的方程；

(2)设曲线y＝f(x)上任一点处的切线的倾斜角为θ，求θ的取值范围

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网