题目内容
已知f(x)是定义在R上且以2为周期的偶函数,当0≤x≤1,f(x)=x2.如果函数g(x)=f(x)-(x+m)有两个零点,则实数m的值为
- A.2k(k∈Z)
- B.2k或2k+
 (k∈Z)
(k∈Z) - C.0
- D.2k或2k-
 (k∈Z)
(k∈Z)
D
分析:利用函数是周期为2的偶函数,作出函数y=f(x)的图象,利用直线y=x+m与曲线y=f(x)恰有两个公共点,利用数形结合的思想求m的值.
解答: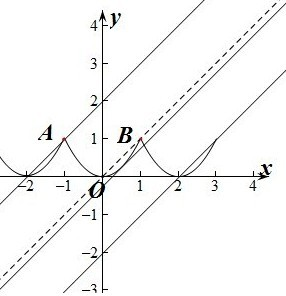 解:由g(x)=f(x)-(x+m)=0得f(x)=(x+m).设y=f(x),y=x+m.
解:由g(x)=f(x)-(x+m)=0得f(x)=(x+m).设y=f(x),y=x+m.
因为f(x)是定义在R上且周期为2的偶函数,所以当-1≤x≤1时,f(x)=x2.
①由图象可知当直线y=x+m经过点O(0,0)时,直线y=x+a与y=f(x)恰有两个公共点,此时m=0,由于函数f(x)是周期为2的函数,所以当m=2k时(k∈Z),
直线y=x+m与曲线y=f(x)恰有两个公共点.
②由图象可知直线y=x+m与f(x)=x2相切时,直线y=x+m与曲线y=f(x)也恰有两个公共点.
f'(x)=2x,由f'(x)=2x=1,解得x= ,所以y=
,所以y= ,即切点为(
,即切点为(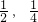 ),
),
代入直线y=x+m得m= .
.
由于函数f(x)是周期为2的函数,所以当m=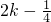 时(k∈Z),直线y=x+m与曲线y=f(x)恰有两个公共点.
时(k∈Z),直线y=x+m与曲线y=f(x)恰有两个公共点.
综上满足条件的实数m的值为m=2k或m=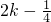 时(k∈Z).
时(k∈Z).
故选D.
点评:本题考查了两个曲线的交点问题,要充分利用函数的周期性,利用数形结合的思想去解决,综合性较强.
分析:利用函数是周期为2的偶函数,作出函数y=f(x)的图象,利用直线y=x+m与曲线y=f(x)恰有两个公共点,利用数形结合的思想求m的值.
解答:
 解:由g(x)=f(x)-(x+m)=0得f(x)=(x+m).设y=f(x),y=x+m.
解:由g(x)=f(x)-(x+m)=0得f(x)=(x+m).设y=f(x),y=x+m.因为f(x)是定义在R上且周期为2的偶函数,所以当-1≤x≤1时,f(x)=x2.
①由图象可知当直线y=x+m经过点O(0,0)时,直线y=x+a与y=f(x)恰有两个公共点,此时m=0,由于函数f(x)是周期为2的函数,所以当m=2k时(k∈Z),
直线y=x+m与曲线y=f(x)恰有两个公共点.
②由图象可知直线y=x+m与f(x)=x2相切时,直线y=x+m与曲线y=f(x)也恰有两个公共点.
f'(x)=2x,由f'(x)=2x=1,解得x=
 ,所以y=
,所以y= ,即切点为(
,即切点为(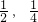 ),
),代入直线y=x+m得m=
 .
.由于函数f(x)是周期为2的函数,所以当m=
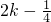 时(k∈Z),直线y=x+m与曲线y=f(x)恰有两个公共点.
时(k∈Z),直线y=x+m与曲线y=f(x)恰有两个公共点.综上满足条件的实数m的值为m=2k或m=
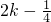 时(k∈Z).
时(k∈Z).故选D.
点评:本题考查了两个曲线的交点问题,要充分利用函数的周期性,利用数形结合的思想去解决,综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目